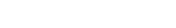Procedural sphere defects
I was writing some code to create a spherical mesh, however it has some odd defects such as:
This spiral going from one pole to the other
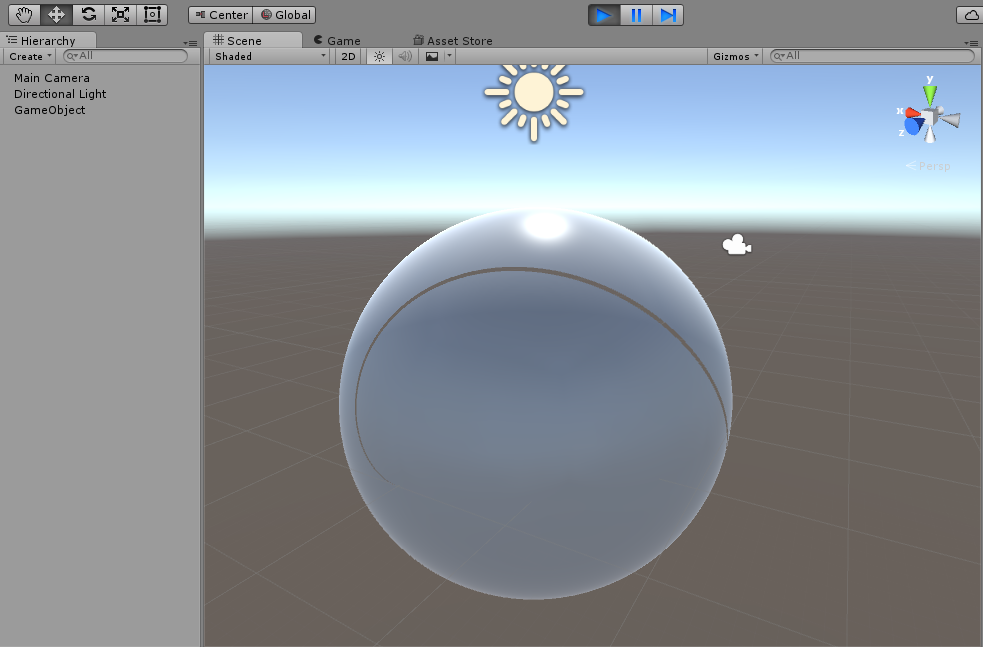
This odd zone across the equator:
I was wandering what is causing those issues. This is the code used to generate the sphere:
using UnityEngine;
using System.Collections;
public class ProceduralSphere : MonoBehaviour {
MeshFilter meshFilter;
Mesh mesh;
Vector3[] vertices;
int[] triangles;
public int N;
public float radius;
// Use this for initialization
void Start () {
meshFilter = GetComponent<MeshFilter>();
mesh = new Mesh();
mesh.name = "ProceduralSphere v1";
vertices = new Vector3[(N + 1) * N];
triangles = new int[N * N * 6];
GenerateSphere(N);
}
// Update is called once per frame
void Update () {
}
void GenerateSphere(int N){
//Generate sphere vertices
int vertCount = 0;
for(int i=0;i<=N;i++){
for(int j=0;j<N;j++){
vertices[vertCount] = SpherePoint(i, j);
vertCount++;
}
}
//Generate triangles from vertices
int triCount = 0;
vertCount = 0;
for(int i=0;i<N-1;i++){
for(int j=0;j<N;j++){
triangles[triCount] = vertCount;
triangles[triCount + 1] = vertCount + N + 1;
triangles[triCount + 2] = vertCount + 1;
triangles[triCount + 3] = vertCount + 1;
triangles[triCount + 4] = vertCount + N + 1;
triangles[triCount + 5] = vertCount + N + 2;
triCount += 6;
vertCount++;
}
vertCount++;
}
mesh.vertices = vertices;
mesh.triangles = triangles;
mesh.Optimize();
mesh.RecalculateNormals();
meshFilter.mesh = mesh;
}
Vector3 SpherePoint(int m, int n){
//(x, y, z) = (sin(Pi * m/M) cos(2Pi * n/N), sin(Pi * m/M) sin(2Pi * n/N), cos(Pi * m/M))
return new Vector3(Mathf.Sin(Mathf.PI*m/N)*Mathf.Cos(2*Mathf.PI*n/N)*radius,
Mathf.Sin(Mathf.PI m/N)*Mathf.Sin(2*Mathf.PI*n/N)*radius,
Mathf.Cos(Mathf.PI*m/N)*radius);
}
}
Answer by Bunny83 · Nov 24, 2015 at 04:27 AM
I would suspect the vertCount++; in line 56 since it seems to be pointless. You also seem to want a fully shared sphere (except for the poles) since you don't have an additional column vertices. In that case your triangle indices are wrong. You should use i and j to calculate the actual index since you need to wrap i value around at when reaching the end of a ring. For this you should remove the "-1" on the limit of your for loop. If you don't wrap it around back to 0 you basically step into the next ring. The gap comes from the "-1". You actually need N*N triangles but currently you only generate N*(N-1) which is where the gap comes from.
It's a bit hard to wrap my head around your coordinates. The triangle generation should look something like that
for(int j=0;j<N;j++){
for(int i=0;i<N;i++){
int offset = j*N;
triangles[triCount++] = offset + i;
triangles[triCount++] = offset + (i + 1)%N;
triangles[triCount++] = offset + N + (i + 1)%N;
triangles[triCount++] = offset + i;
triangles[triCount++] = offset + N + (i + 1)%N;
triangles[triCount++] = offset + N + i;
}
}
The modulo operator will make the expression in brackets wrap around back to 0 at the end. Here's an example of 8 values:
i (i + 1)%N
-------------------
0 1
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 0
Note how the last "i+1" will wrap back to 0 instead of resulting in 9. That way you stay on the current ring instead of jumping down to the next.
Thank you, indeed the issue was the way I created the triangles, however, I changed the order of the vertices from the code snippet you posted because I need the sphere to be visible from the outside:`triangles[triCount++] = offset + i; triangles[triCount++] = offset + N + (i + 1)%N; triangles[triCount++] = offset + (i + 1)%N;
triangles[triCount++] = offset + i;
triangles[triCount++] = offset + N + i;
triangles[triCount++] = offset + N + (i + 1)%N;`
Sure, as i said it's hard to wrap my head around the way you arranged your vertices. However i thought i had them right. However i just realised that your sphere doesn't stand up right. You have the poles in z direction. That's what i missed. Usually you would create the rings in the x-z plane and let the rings go down the y axis.
Your answer