How to draw walls around rooms using the least number of objects for walls?

I have created a new project to test in before I implement it into my game. Essentially my end game will have a series of rooms. I want to generate all the walls around each room via code. I would really appreciate some help in working this problem out. The current code I have does the follow:

1. Randomly generate a floor tile from 1 to 3
2. Place an coloured object to indicate the floor tile's number
3. Place a along wall on the north, south, east and west sides of the base cube
4. Loop through each tile and work out if the one before (either in x for horizontal, or y for vertical) and place a wall if the tile before is different than the current one.

What I want to do to optimise this all is only use a single object for continuous sides. For example: In the current code, a wall may consist of 3 single wall items in a row one after the other. I want it to just make 1 wall instead to replace these 3 walls.

So basically optimising it this way:

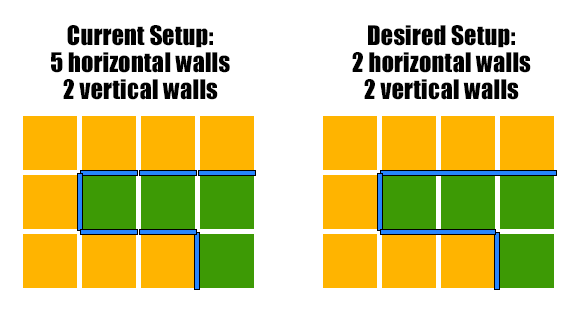
Here is what my current setup looks like:

And here is the code I have for the above current setup:

 using System.Collections;
 using System.Collections.Generic;
 using UnityEngine;
 
 public class Walls : MonoBehaviour {
 
     int[,] tiles;
     public GameObject wall;
     public Transform walls;
 
     public GameObject floor1;
     public GameObject floor2;
     public GameObject floor3;
     public GameObject floor;
 
     public int width = 30;
     public int height = 30;
 
     void Start () {
         tiles = new int[width,height];
         GenerateTiles();
         GenerateWalls();
     }
 
     void GenerateTiles() {
         for(int x = 0; x < width; x++) {
             for(int y = 0; y < height; y++) {
                 tiles[x,y] = Random.Range(1,4);
             }
         }
     }
 
     void GenerateWalls() {
         Vector3 horizontal = new Vector3(0,0,0);
         Vector3 vertical = new Vector3(0,90,0);
         GameObject northWall = Instantiate(wall,new Vector3(0,-0.5f,(height / 2)),Quaternion.Euler(horizontal),walls);
         northWall.transform.localScale += new Vector3(width - 1,0,0);
         GameObject southWall = Instantiate(wall,new Vector3(0,-0.5f,-(height / 2)),Quaternion.Euler(horizontal),walls);
         southWall.transform.localScale += new Vector3(width - 1,0,0);
         GameObject eastWall = Instantiate(wall,new Vector3((width / 2),-0.5f,0),Quaternion.Euler(vertical),walls);
         eastWall.transform.localScale += new Vector3(width - 1,0,0);
         GameObject westWall = Instantiate(wall,new Vector3(-(width / 2),-0.5f,0),Quaternion.Euler(vertical),walls);
         westWall.transform.localScale += new Vector3(width - 1,0,0);
         for(int x = 0; x < width; x++) {
             for(int y = 0; y < height; y++) {
                 if(tiles[x,y] == 1) {
                     GameObject newFloorTile = Instantiate(floor1,new Vector3(x - (width/2) + 0.5f,-0.5f,y - (height/2) + 0.5f),transform.rotation,floor.transform);
                 }
                 if(tiles[x,y] == 2) {
                     GameObject newFloorTile = Instantiate(floor2,new Vector3(x - (width / 2) + 0.5f,-0.5f,y - (height / 2) + 0.5f),transform.rotation,floor.transform);
                 }
                 if(tiles[x,y] == 3) {
                     GameObject newFloorTile = Instantiate(floor3,new Vector3(x - (width / 2) + 0.5f,-0.5f,y - (height / 2) + 0.5f),transform.rotation,floor.transform);
                 }
                 if(y != 0 && y != height) {
                     if(tiles[x,y-1] != tiles[x,y]) {
                         GameObject xWall = Instantiate(wall,new Vector3(x - (width / 2) + 0.5f,-0.5f,y - (height / 2)),Quaternion.Euler(horizontal),walls);
                     }
                 }
                 if(x != 0 && x != width) {
                     if(tiles[x - 1,y] != tiles[x,y]) {
                         GameObject yWall = Instantiate(wall,new Vector3(x - (width / 2),-0.5f,y - (height / 2) + 0.5f),Quaternion.Euler(vertical),walls);
                     }
                 }
             }
         }
     }
 }