- Home /
2D Vectors along 3D Triangle
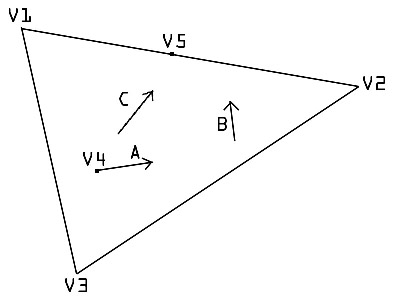
So I thought I should include this picture to demonstrate what I've been trying to figure out how to do, but not having any luck googling, checking answers, boards, etc.
V1-V5 are Vector3's
A,B,C are Vector2's
So I'm trying to split a triangle along a certain path.
V4 is the starting Vector3
A is the starting Direction
I want to askew A according to B to get C, (adding them then normalizing, easy)
And using C from V4 to find the intersection point V5 giving a length (this will be tested to find if/which edge the resulting vector hits. This is on a Mesh, so I have access to the normals of V1,V2, and V3, so I feel like I should be able to bring the problem down to 2 dimensions, then bring it back to 3D once I have the answer.... but I'm not sure. Anyone have any ideas?
As I understand this, you want to find the point at which the line V4 + C intersects the line V1->V2. You've not explained what the vectors A, B, and C are, so I'm not sure if V4 + C is in the same plane as the triangle?
If they are in the same plane, its a simple case of calculating that intersection. If they're not, then they won't intersect, and perhaps that's why your asking about doing it in 2D? In that case you first need to project the vector C into the plane of the triangle, and then intersect. If you can clarify that, I'll see if I can help with the actual math.
Like in the question, A,B,C are Vector2's. I'm trying to use them as directional vector's along the triangle plane. They have no depth, so yes, they will be on the plane. $$anonymous$$ind of like how UVs (2D Vectors) are used to map textures on 3D triangles. And yes, that is precisely what I'm trying to do, project the 2D vectors onto the triangle.
You say two things that aren't compatible:
The Vector2s are on the plane of the triangle
You want to project the 2D vectors onto the triangle
Which is correct?
Perhaps this is confusion from semantics. The Vector2s are directions. Think of them as Vector3's with 0 as the z value. Their 'up', will be the normal of the Triangle plane. I want to use them, to find point V5.
Ins$$anonymous$$d of projecting the Vec2s onto the polygon, have you tried flattening the polygon onto the Vec2s?
Rotate the poly around V4 until its normal == Vector3.up. (or alternately until its Z values are the same, so you can use the Vector3s without translating them to Vector2s first). You'd have to translate V4 into a Vector3 first, then it'd be something like (V1 = (V1-V4)*rotation + V4).
Quaternion.FromToRotation might help; you can rotate a point with v3 * quat.
Edit: Oh yeah, get the rotation using FromToRotation - rotate from poly's normal to desired normal.
Your answer