- Home /
Normalizing several meshes towards a sphere.
Hello everyone.
I'm trying to make a planet out of a normalized cube. I've successfully normalized the cube into a sphere by having 6 different meshes, one for each side of the cube, by normalizing the vertices.
From my point of view, using this method, and considering the (approx) 64000 vertices limit for each mesh, the planet becomes rather small.
That being said, I am attempting to make one side of the cube out of 4 separate meshes. I successfully created 4 different meshes and centered them in 0, 0, 0 coordinates. However, when I go for normalizing the said meshes, it doesn't normalize it properly as in the 4 meshes are normalized separately. I'm adding some images for you to understand what I mean.
Thanks a lot in advance ;)
P.S.: I'm only trying to normalize the top face of the cube. 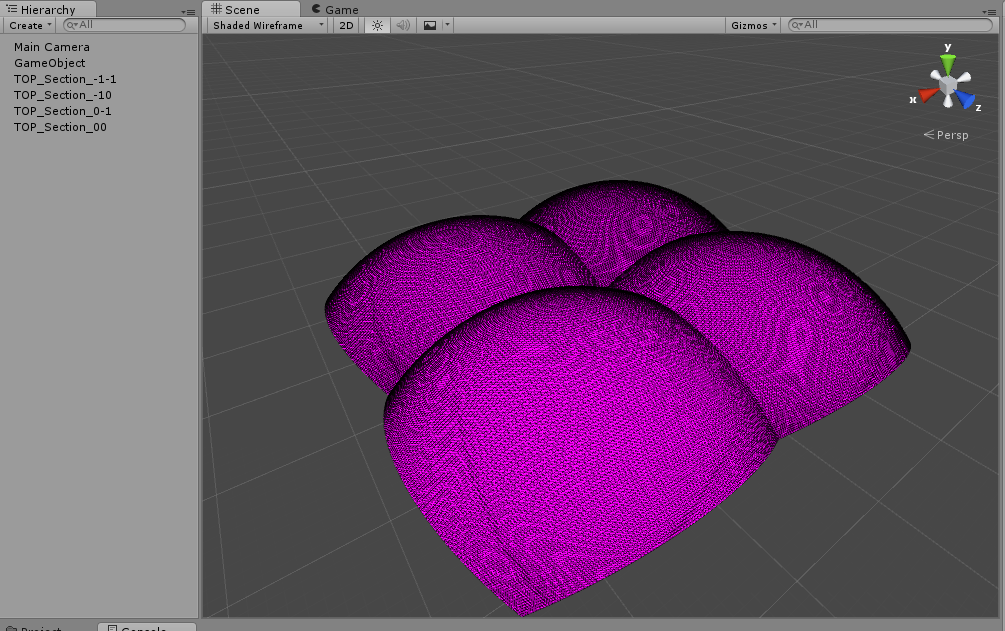
What do you mean by "normalize? In Unity lingo, normaliazing means to clamp a value between 0 and 1.
As it is to my understanding, one can obtain a sphere by normalizing every vertex from the faces of a cube and by multiplying the normalized vertex value by the série d radius of the sphere. That is what I mean by normalizing.
Answer by Bunny83 · Oct 07, 2015 at 05:13 PM
Well, before you normalize your vertex position you have to transform them into a common space. So for example if you have an empty gameobject "center" in the center of your sphere, you have to do this for each patch:
// C#
Vector3 pos = center.InverseTransformPoint(patch.TransformPoint(vertex));
pos = pos.normalized * radius;
vertex = patch.InverseTransformPoint(center.TransformPoint(pos));
"patch" is the Transform component of each mesh and "vertex" is one local space vertex of a mesh.
edit
Here's a simple script that can create an arbitrarily large planet mesh (as long as your hardware can handle it). As mentioned below it creates child object for each mesh. Those objects origins are all at the cube / sphere center. We just calculate the vertices in each patch relative to it's target position inside our cube.
using UnityEngine;
using System.Collections;
public struct PatchConfig
{
public string name;
public Vector3 uAxis;
public Vector3 vAxis;
public Vector3 height;
public PatchConfig(string aName, Vector3 aUAxis, Vector3 aVAxis)
{
name = aName;
uAxis = aUAxis;
vAxis = aVAxis;
height = Vector3.Cross(vAxis, uAxis);
}
}
public class PlanetMesh : MonoBehaviour
{
private static PatchConfig[] patches = new PatchConfig[]
{
new PatchConfig("top", Vector3.right, Vector3.forward),
new PatchConfig("bottom", Vector3.left, Vector3.forward),
new PatchConfig("left", Vector3.up, Vector3.forward),
new PatchConfig("right", Vector3.down, Vector3.forward),
new PatchConfig("front", Vector3.right, Vector3.down),
new PatchConfig("back", Vector3.right, Vector3.up)
};
public int uPatchCount = 2;
public int vPatchCount = 2;
public int xVertCount = 250;
public int yVertCount = 250;
public float radius = 5f;
public Material patchMaterial;
void Start ()
{
GeneratePatches();
}
void GeneratePatch(PatchConfig aConf, int u, int v)
{
GameObject patch = new GameObject("Patch_" + aConf.name + "_" + u + "_" + v);
MeshFilter mf = patch.AddComponent<MeshFilter>();
MeshRenderer rend = patch.AddComponent<MeshRenderer>();
rend.sharedMaterial = patchMaterial;
Mesh m = mf.sharedMesh = new Mesh();
patch.transform.parent = transform;
patch.transform.localEulerAngles = Vector3.zero;
patch.transform.localPosition = Vector3.zero;
Vector2 UVstep = new Vector2(1f / uPatchCount, 1f / vPatchCount);
Vector2 step = new Vector2(UVstep.x / (xVertCount-1), UVstep.y / (yVertCount-1));
Vector2 offset = new Vector3((-0.5f + u * UVstep.x), (-0.5f + v * UVstep.y));
Vector3[] vertices = new Vector3[xVertCount * yVertCount];
Vector3[] normals = new Vector3[vertices.Length];
Vector2[] uvs = new Vector2[vertices.Length];
for (int y = 0; y < yVertCount; y++)
{
for (int x = 0; x < xVertCount; x++)
{
int i = x + y * xVertCount;
Vector2 p = offset + new Vector2(x * step.x, y * step.y);
uvs[i] = p + Vector2.one*0.5f;
Vector3 vec = aConf.uAxis * p.x + aConf.vAxis * p.y + aConf.height*0.5f;
vec = vec.normalized;
normals[i] = vec;
vertices[i] = vec*radius;
}
}
int[] indices = new int[(xVertCount - 1) * (yVertCount - 1) * 4];
for (int y = 0; y < yVertCount-1; y++)
{
for (int x = 0; x < xVertCount-1; x++)
{
int i = (x + y * (xVertCount-1)) * 4;
indices[i] = x + y * xVertCount;
indices[i + 1] = x + (y + 1) * xVertCount;
indices[i + 2] = x + 1 + (y + 1) * xVertCount;
indices[i + 3] = x + 1 + y * xVertCount;
}
}
m.vertices = vertices;
m.normals = normals;
m.uv = uvs;
m.SetIndices(indices, MeshTopology.Quads, 0);
m.RecalculateBounds();
}
void GeneratePatches()
{
for(int i = 0; i < 6; i++)
{
for(int u = 0; u < uPatchCount; u++)
{
for(int v = 0; v < vPatchCount; v++)
{
GeneratePatch(patches[i], u, v);
}
}
}
}
}
Note: the orientation of each cube side is determined by the patches array. The UVs are calculated per cube side. So no matter if you "subdivide" each side further one side will always be in range [0,1]
@Bunny83, first of all, thanks for your answer.
I did as you suggested and I got what is shown in the image. It did the proper spherifying thingy now but it seems it is rather diverted from the center point as in, in the image, the sections should cover the entirety of the "top" side of the sphere, but it only covers a part of it.
Any thoughts? Thanks once again. 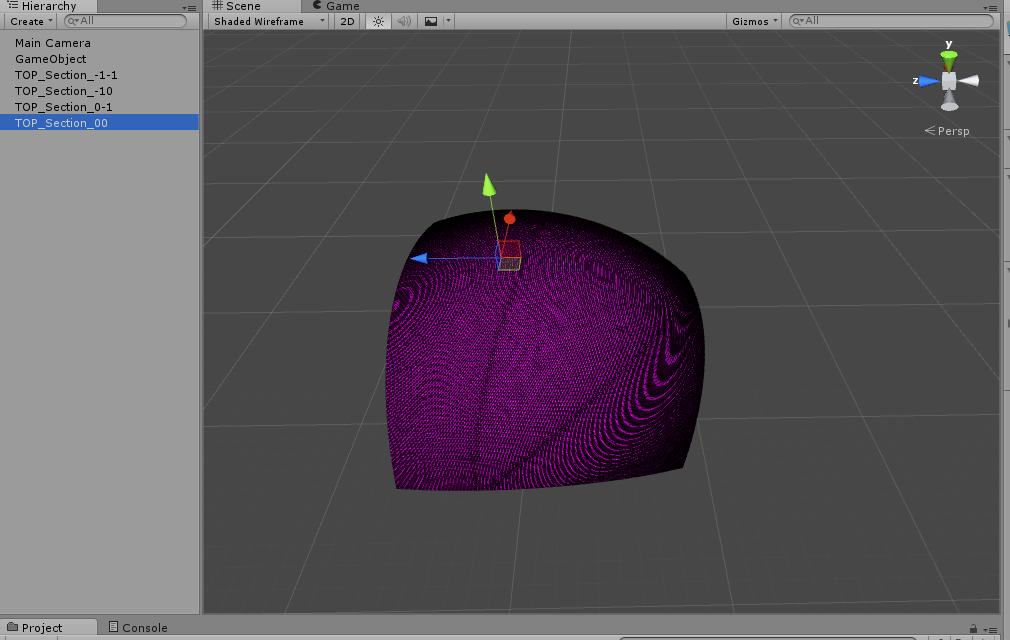
$$anonymous$$aybe i should add that if you create the whole thing procedurally, you don't need to do this for each vertex when you simply offset the vertices when you create them. That means your would place the gameobject for all 24 patches (4 each side * 6 sides) at the center of your cube / sphere. When you create the vertices for the mesh you don't generate them around the local center, but at their respective position in your final cube.
I've just written a simple script that can create a procedural planet mesh of arbitrary size. I'll add it to my answer above.
@Bunny83, sorry for only answering today, it has been a long end of the week.
Thanks a lot for your help, including giving me your code. I was attempting to do something like this but it got no where as good as yours. Thanks once again.
Your answer


