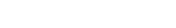- Home /
Smooth movement along an uneven surface
Hi,
I'm experimenting with moving a round object along various curved surfaces (circles and bends, etc). I'm using the method of raycasting to get the surface normal and then inverting it and using that as either a downward force or setting gravity in that direction (after normalizing/multiplying the vector). Both work ok but since I'm using polygons, the round object kind of bumps along the surface (see picture).
Using gravity I got smoother results but I was wondering if there were any other solutions apart from maybe a smoother collision mesh?
Here's some pictures using the trail renderer to show the bumps.
With Force 
With Gravity 
Could you not just get a vector that points to the centre of your "planet" and apply a "gravity" force towards it? (ie: via AddForce, as opposed to changing gravity, or is that what you are doing?)
Did you consider a sphere collider?
When you use the sphere, does your "planet" have a mesh collider too? It could be that the bumpiness is caused by the planet's collider poking through in places.
A sphere collider should be a perfect sphere since I assume it works by distance vectors (to be fast) as opposed to a bumpy mesh. Perhaps if you made the sphere very slightly bigger than the planet it would fix it? I'm not sure of the nature of your game, of course, so that might not be appropriate.
As for the L-shapes... Hmmm... Have to think about that :/
Answer by markTheDesigner · Mar 01, 2013 at 04:35 PM
Hi, yes that possible (and I'll try that for the completely round platforms) but some platforms are L shaped (like a pipe curving upwards) so their centre will be in an odd place. So that won't work for that.
Yup, I'm using a sphere collider but even that is not perfectly round (at least it's not visibly perfectly round in Unity). I zoomed in to see why the bumps were happening and the sphere actually goes though the surface of the 'planet' just a little bit after each face. I've fiddled with the physics properties but nothing makes it any better. I guess what happens is that after each peak (the angle difference between each face) the sphere realigns, via the normals calculation and then pushes back into the 'planet'. Maybe if I play around with the strength of gravity it won't be so obvious. The Sphere (moving object) is 1m size btw, if it makes any difference.
Your answer