- Home /
Can someone explain why the angle between the Normal and Global Up equals the angle of the slope of the ground?
So I have a simple platform 2D project going on in Unity at the moment and I'm following a tutorial on how to get the player GameObject to travel up angled slopes. Part of the tutorial involves calculating the angle of the slope of the ground that the Player GameObject is walking on. You do this by firing a raycast from the right bottom corner of the Player GO and then get the Normal of the collision between the raycast and the ground. In the tutorial the guy states that you can then calculate the angle between between the Normal and Global Up by using Vector2.Angle.
This angle happens to also equal the angle of the slope that the player GO is moving on but I don't understand why this is? Does it have something to do with the Pythagoras Theorem? Can someone explain what I ask in simple terms? Thanks
Answer by Hellium · Apr 13, 2021 at 07:48 PM
Because a picture is worth a thousand words:
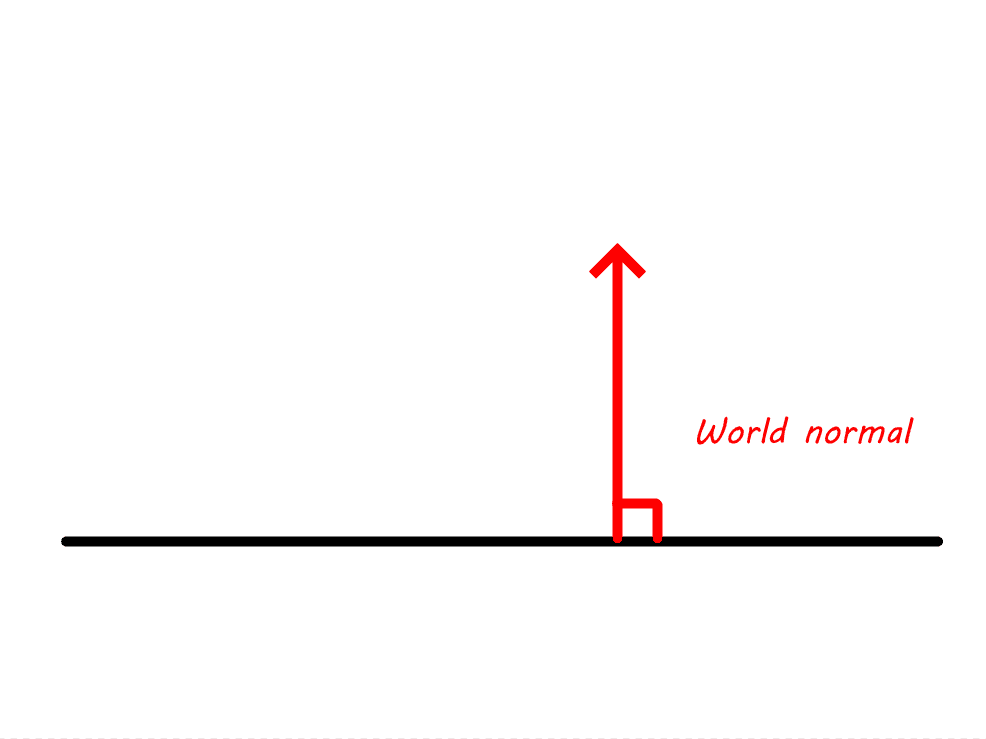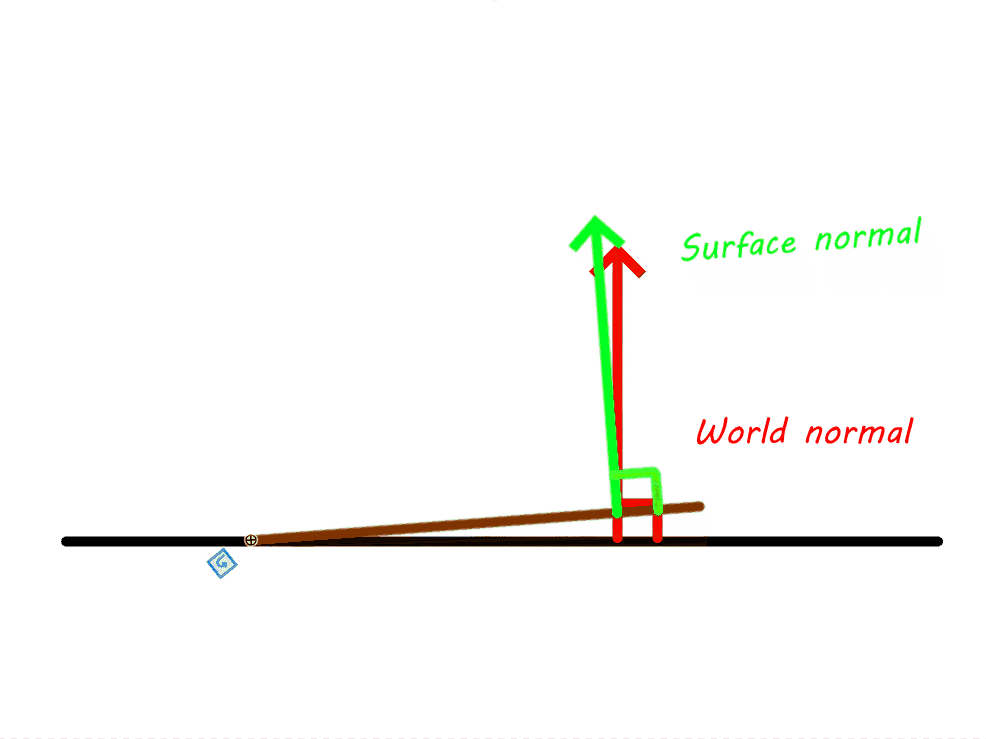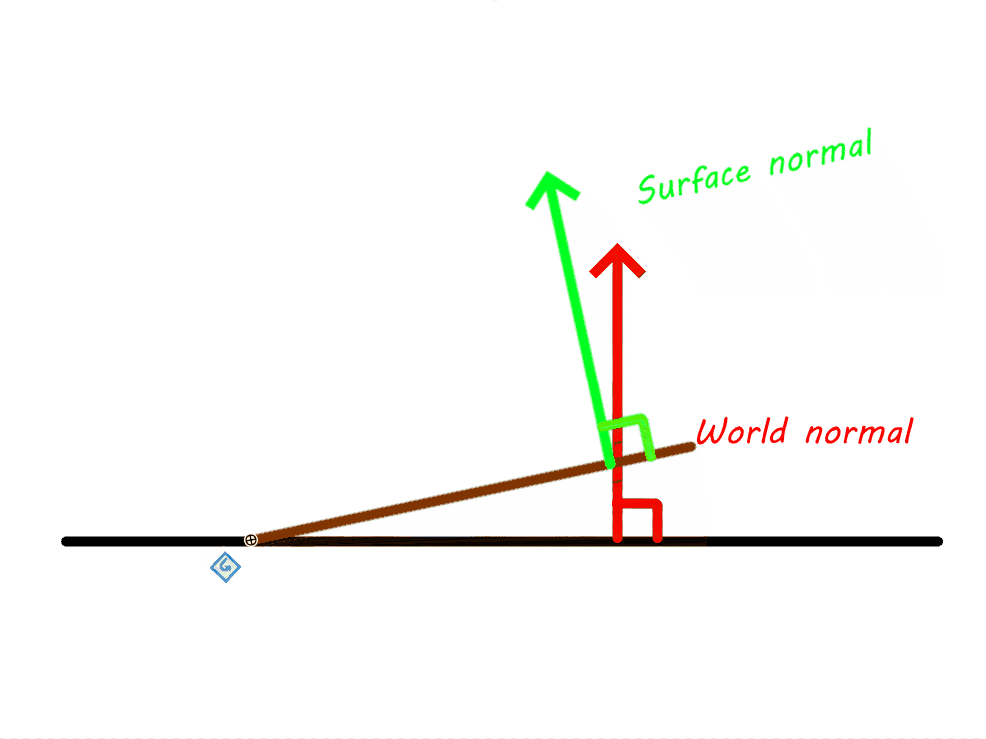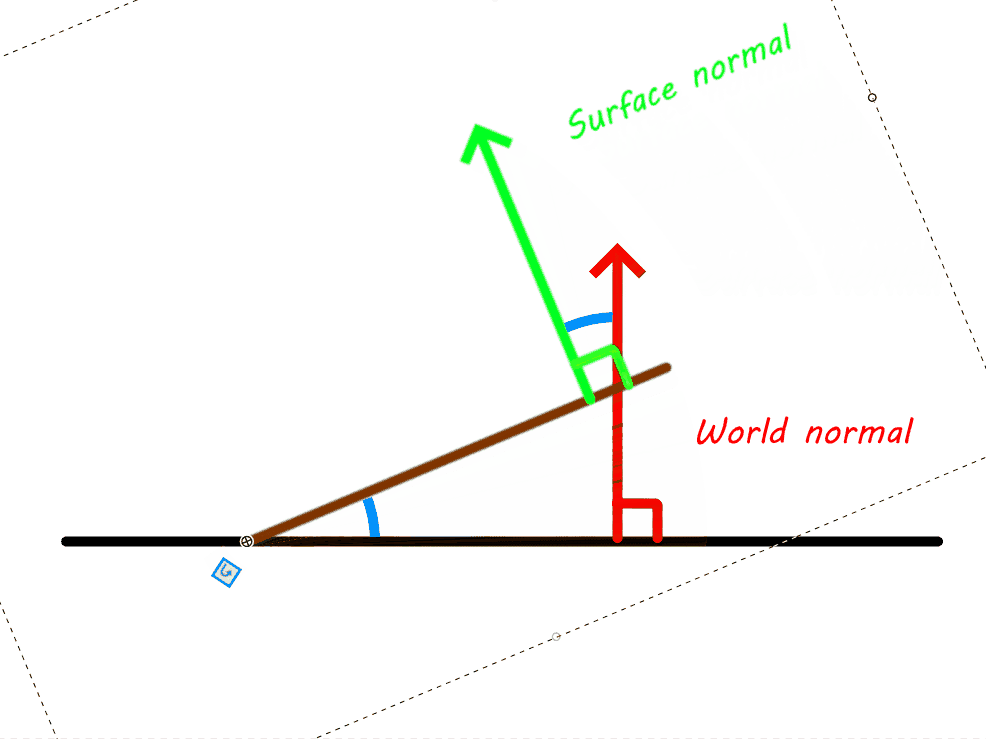
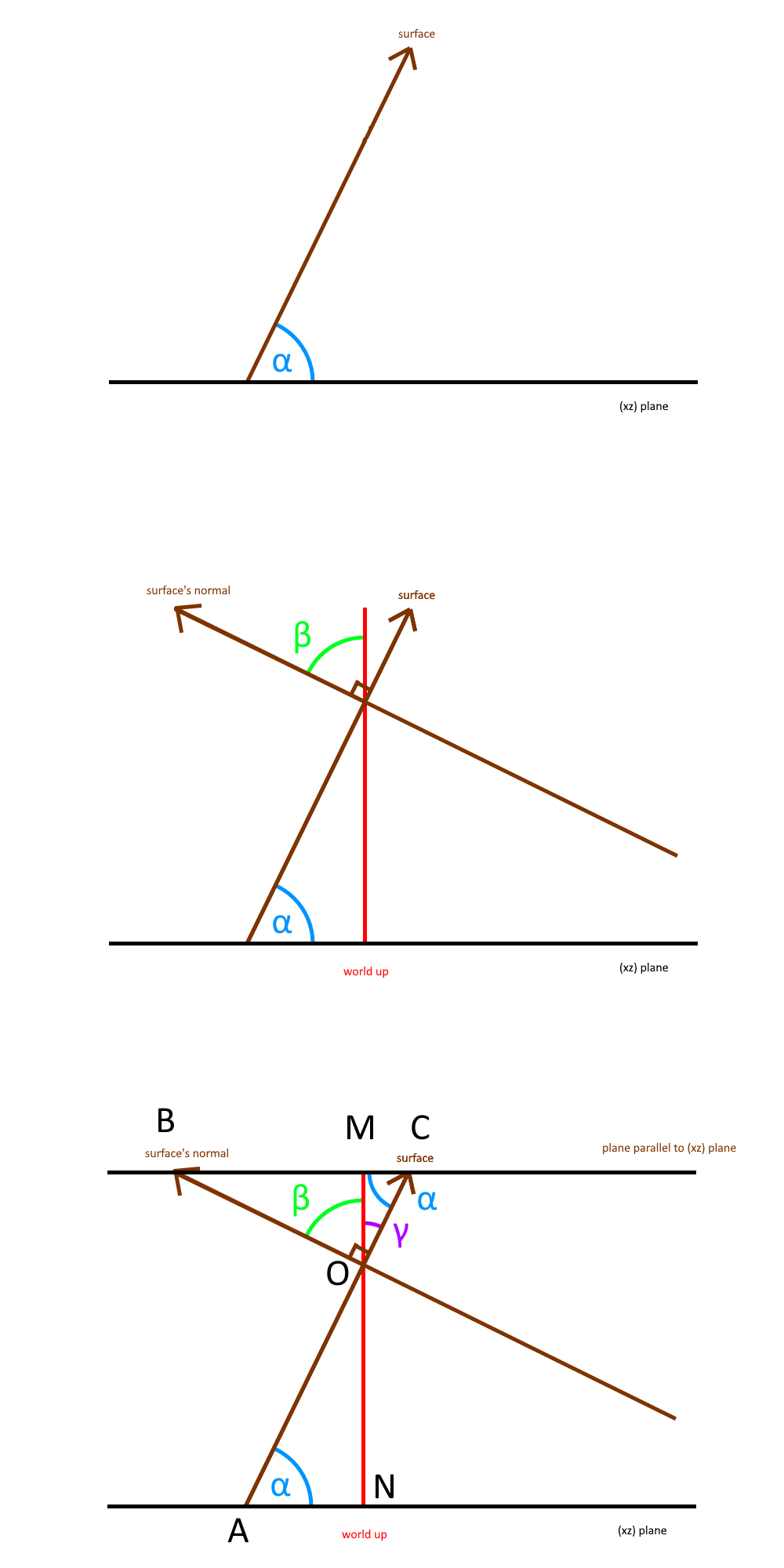
For a scientific proof:
Let's draw an imaginary plane parallel to the (xz) plane.
Let's be:
- A, the intersection point between the surface and the world's (xz) plane.
- C the intersection point between the surface and the imaginary plane parallel to the (xz) plane
- O the intersection point between the surface and its normal
- B the intersection point between the surface's normal and the imaginary plane
- N the intersection point between the (xz) plane and the world Y vector going through O
- M the intersection point between the imaginary plane and the world Y vector going through O
- α the angle between the (xz) plane and the surface: α = NAO
- β is the angle between the surface's normal and the world (global) Y vector β = MOB
- γ is the angle between the surface and the world Y vector γ = MOC
(see 3rd drawing below).
Thanks to the parallel lines theorems, we know that the alternate interior angles are equal, i.e MCO = NAO = α and that OMC = 90°
We also know that the sum of the angles of a triangle equals 180° so MCO + COM + OMC = 180° ⇔ α + γ + 90° = 180° ⇔ γ = 90° - α.
We also know that BOM + MOC = BOC ⇔ β + γ = 90°
If we replace γ = 90° - α in β + γ = 90°, we end up with β + (90° - α) = 90° ⇔ β = α
Okay I accept that the angles are the same but what makes them the same? How are they proven to be the same? How do we know for sure?
@egonspengler_84 I've added the scientific proof with drawings, theorems and calculus
Your answer