- Home /
Affine transformations to Object
Hello. I am trying to make an application to calculate the 2D affine transformation of an object, but not only the standard transformations (translation, rotation, scaling, etc), I want the user to be able to input any number in 9 text fields (a 3x3 matrix) and for the object to transform based on those numbers. The object is square shaped. This is the formula I wil be using:
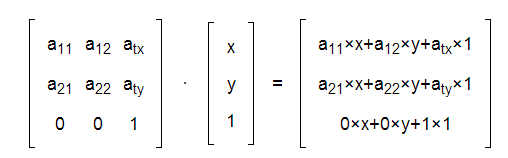
Where the matrix with the "a"s is my affine transformation matrix (where the user will be inputting) and the x and y have to be calculated for each of the four points that limit my square. Now, my question is, to what values should I assign the position, rotation, and scaling properties of my Unity object, considering that those four points could be anywhere on my plane? I am aware that this is a mathematical question more than a Game Development question; however I am using Unity for my application would like to know if someone can help me with this. Thanks!
Answer by Scribe · Apr 29, 2014 at 12:05 AM
Okay so here is a Matrix3x3 class, you could quite easily add a lot more function for other things, but I think what I have done will suffice as a good start, so the main class:
using UnityEngine;
using System.Collections;
public class Matrix3x3{
public static Matrix3x3 identity = new Matrix3x3(1, 0, 0, 0, 1, 0, 0, 0, 1);
public static Matrix3x3 zero = new Matrix3x3(0, 0, 0, 0, 0, 0, 0, 0, 0);
public float[,] matrix;
public Matrix3x3(){
matrix = new float[3, 3];
matrix[0, 0] = 0;
matrix[1, 0] = 0;
matrix[2, 0] = 0;
matrix[0, 1] = 0;
matrix[1, 1] = 0;
matrix[2, 1] = 0;
matrix[0, 2] = 0;
matrix[1, 2] = 0;
matrix[2, 2] = 0;
}
public Matrix3x3(float a11, float a12, float a13, float a21, float a22, float a23){
matrix = new float[3, 3];
matrix[0, 0] = a11;
matrix[1, 0] = a12;
matrix[2, 0] = a13;
matrix[0, 1] = a21;
matrix[1, 1] = a22;
matrix[2, 1] = a23;
matrix[0, 2] = 0;
matrix[1, 2] = 0;
matrix[2, 2] = 1;
}
public Matrix3x3(Vector3 a1, Vector3 a2){
matrix = new float[3, 3];
matrix[0, 0] = a1.x;
matrix[1, 0] = a1.y;
matrix[2, 0] = a1.z;
matrix[0, 1] = a2.x;
matrix[1, 1] = a2.y;
matrix[2, 1] = a2.z;
matrix[0, 2] = 0;
matrix[1, 2] = 0;
matrix[2, 2] = 1;
}
public Matrix3x3(float a11, float a12, float a13, float a21, float a22, float a23, float a31, float a32, float a33){
matrix = new float[3, 3];
matrix[0, 0] = a11;
matrix[1, 0] = a12;
matrix[2, 0] = a13;
matrix[0, 1] = a21;
matrix[1, 1] = a22;
matrix[2, 1] = a23;
matrix[0, 2] = a31;
matrix[1, 2] = a32;
matrix[2, 2] = a33;
}
//MATRIX MULTIPLICATION
public static Matrix3x3 operator *(Matrix3x3 m1, Matrix3x3 m2){
float a11 =
m1.matrix[0, 0] * m2.matrix[0, 0] +
m1.matrix[1, 0] * m2.matrix[0, 1] +
m1.matrix[2, 0] * m2.matrix[0, 2];
float a12 =
m1.matrix[0, 0] * m2.matrix[1, 0] +
m1.matrix[1, 0] * m2.matrix[1, 1] +
m1.matrix[2, 0] * m2.matrix[1, 2];
float a13 =
m1.matrix[0, 0] * m2.matrix[2, 0] +
m1.matrix[1, 0] * m2.matrix[2, 1] +
m1.matrix[2, 0] * m2.matrix[2, 2];
float a21 =
m1.matrix[0, 1] * m2.matrix[0, 0] +
m1.matrix[1, 1] * m2.matrix[0, 1] +
m1.matrix[2, 1] * m2.matrix[0, 2];
float a22 =
m1.matrix[0, 1] * m2.matrix[1, 0] +
m1.matrix[1, 1] * m2.matrix[1, 1] +
m1.matrix[2, 1] * m2.matrix[1, 2];
float a23 =
m1.matrix[0, 1] * m2.matrix[2, 0] +
m1.matrix[1, 1] * m2.matrix[2, 1] +
m1.matrix[2, 1] * m2.matrix[2, 2];
float a31 =
m1.matrix[0, 2] * m2.matrix[0, 0] +
m1.matrix[1, 2] * m2.matrix[0, 1] +
m1.matrix[2, 2] * m2.matrix[0, 2];
float a32 =
m1.matrix[0, 2] * m2.matrix[1, 0] +
m1.matrix[1, 2] * m2.matrix[1, 1] +
m1.matrix[2, 2] * m2.matrix[1, 2];
float a33 =
m1.matrix[0, 2] * m2.matrix[2, 0] +
m1.matrix[1, 2] * m2.matrix[2, 1] +
m1.matrix[2, 2] * m2.matrix[2, 2];
return new Matrix3x3(a11, a12, a13, a21, a22, a23, a31, a32, a33);
}
//FLOAT MULTIPLICATION
public static Matrix3x3 operator *(Matrix3x3 m, float f){
for(int i = 0; i < 3; i++){
for(int j = 0; j < 3; j++){
m.matrix[i, j] *= f;
}
}
return m;
}
public static Matrix3x3 operator *(float f, Matrix3x3 m){
for(int i = 0; i < 3; i++){
for(int j = 0; j < 3; j++){
m.matrix[i, j] *= f;
}
}
return m;
}
//ToSTRING OVERRIDE
public override string ToString(){
string str = "[";
for(int i = 0; i < 3; i++){
for(int j = 0; j < 3; j++){
str += matrix[j, i].ToString();
str += i*j == 4 ? "]" : ", ";
}
}
return str;
}
}
public static class ExtensionMethods{
public static Vector3 MultiplyPoint(this Matrix3x3 m, Vector3 point){
Vector3 newPoint;
newPoint.x = m.matrix[0, 0]*point.x + m.matrix[1, 0]*point.y + m.matrix[2, 0];
newPoint.y = m.matrix[0, 1]*point.x + m.matrix[1, 1]*point.y + m.matrix[2, 1];
newPoint.z = point.z;
return newPoint;
}
public static Vector3 MultiplyVector(this Matrix3x3 m, Vector3 vec){
Vector3 newVec;
newVec.x = m.matrix[0, 0]*vec.x + m.matrix[1, 0]*vec.y;
newVec.y = m.matrix[0, 1]*vec.x + m.matrix[1, 1]*vec.y;
newVec.z = vec.z;
return newVec;
}
public static Matrix3x3 Transpose(this Matrix3x3 m){
Matrix3x3 newM = new Matrix3x3();
for(int i = 0; i < 3; i++){
for(int j = 0; j < 3; j++){
newM.matrix[i, j] = m.matrix[j, i];
}
}
return newM;
}
public static Matrix3x3 Inverse(this Matrix3x3 m){
Matrix3x3 newM;
float a11 = m.matrix[0, 0];
float a12 = m.matrix[1, 0];
float a13 = m.matrix[2, 0];
float a21 = m.matrix[0, 1];
float a22 = m.matrix[1, 1];
float a23 = m.matrix[2, 1];
float a31 = m.matrix[0, 2];
float a32 = m.matrix[1, 2];
float a33 = m.matrix[2, 2];
float m11 = (a22*a33)-(a23*a32);
float m12 = (a21*a33)-(a23*a31);
float m13 = (a21*a32)-(a22*a31);
float m21 = (a12*a33)-(a13*a32);
float m22 = (a11*a33)-(a13*a31);
float m23 = (a11*a32)-(a12*a31);
float m31 = (a12*a23)-(a13*a22);
float m32 = (a11*a23)-(a13*a21);
float m33 = (a11*a22)-(a12*a21);
newM = new Matrix3x3(m11, -m12, m13, -m21, m22, -m23, m31, -m32, m33);
newM = newM.Transpose();
float detM = (m*newM).matrix[0, 0];
if(detM == 0){
Debug.Log("determinant is 0, no inverse could be found (original matrix has been returned)");
return m;
}else{
detM = 1f/detM;
newM = detM*newM;
return newM;
}
}
}
So far I think I have covered creating a 3x3 matrix, invereses, identity, zero matrix, transposing a matrix, multiplying a point and multiplying a vector, as well as some quality of life stuff like operator overloads for easily multiplying matricies by matricies or floats. To get an idea of how to use, check out the following:
Matrix3x3 m;
Matrix3x3 iM;
Matrix3x3 tM;
Matrix3x3 newM;
public Vector3 point;
public Vector3 vector;
void Start(){
m = new Matrix3x3(1, 2, 3, 1, 1, 1, 3, 7, 9);
iM = m.Inverse();
tM = m.Transpose();
Debug.Log("matrix: " + m);
Debug.Log("inverse of matrix: " + iM);
Debug.Log("transpose of matrix: " + tM);
Debug.Log("inverse times matrix: " + m*iM);
Debug.Log("identity matrix: " + Matrix3x3.identity);
Debug.Log("zero matrix: " + Matrix3x3.zero);
m = new Matrix3x3(1, 0, 3, 0, 1, 12);
point = new Vector3(1, 2, 3);
Debug.Log("matrix: " + m);
Debug.Log("point: " + point);
point = m.MultiplyPoint(point);
Debug.Log("transformed point: " + point);
m = new Matrix3x3(new Vector3(2, 3, 4), new Vector3(12, 2, 1));
vector = new Vector3(2, 1, 3);
Debug.Log("matrix: " + m);
Debug.Log("vector: " + vector);
vector = m.MultiplyVector(vector);
Debug.Log("transformed vector: " + vector);
m = new Matrix3x3(1, 2, 3, 1, 1, 1, 3, 7, 9);
Debug.Log("matrix: " + m);
m *= 3;
Debug.Log(" 3 x matrix: " + m);
}
I hope that helps,
Scribe
I should add that for your transformation you would get the corner points and apply yhe matrix with the $$anonymous$$ultiplyPoint method to get your new points, then drawlines between your new points to recreate your shape.
Checkout the $$anonymous$$esh class: http://docs.unity3d.com/Documentation/ScriptReference/$$anonymous$$esh.html I would suggest you grab the positions of your verticies, triangles and normals from your cube object, then change the vertice points using the matrix, then set that to your new deformed mesh. the triangle index and normals for the front face should be able to be kept the same, the other normals might need to be recalculated.
So I had a bit more time to update this, hopefully this will mean you can mark the question as answered:
$$anonymous$$atrix3x3 m;
public Vector3 row1 = Vector3.zero;
Vector3 oldRow1 = Vector3.zero;
public Vector3 row2 = Vector3.zero;
Vector3 oldRow2 = Vector3.zero;
void Start(){
Calc$$anonymous$$atrix();
}
//Update matrix
void Calc$$anonymous$$atrix(){
m = new $$anonymous$$atrix3x3(row1, row2);
}
void Update () {
//Check if the matrix inputs has changed
if(oldRow1 != row1 || oldRow2 != row2){
Calc$$anonymous$$atrix();
oldRow1 = row1;
oldRow2 = row2;
}
//recalculate mesh on Q press
if(Input.Get$$anonymous$$eyDown($$anonymous$$eyCode.Q)){
DeformObj(gameObject);
}
}
//Recalculates the mesh verticies based on matrix operator
void DeformObj(GameObject go){
$$anonymous$$esh mesh = go.GetComponent<$$anonymous$$eshFilter>().mesh;
Vector3[] vertices = mesh.vertices;
int[] vertIndexed = new int[vertices.Length];
for(int v = 0; v < vertices.Length; v++){
if(vertIndexed[v] != 1){
vertices[v] = m.$$anonymous$$ultiplyPoint(vertices[v]);
vertIndexed[v] = 1;
}
}
mesh.vertices = vertices;
mesh.RecalculateNormals();
mesh.RecalculateBounds();
}
That should skew or deform your object mesh as you would expect it to, your overall transform position/rotation/scale will remain 0 however.
If you do get this working please remember to mark the answer as accepted!
Thanks,
Scribe
Sure, just change line 37 (`vertices[v] = m.$$anonymous$$ultiplyPoint(vertices[v]);`) to:
vertices[v] = go.transform.InverseTransformPoint(m.$$anonymous$$ultiplyPoint(go.transform.TransformPoint(vertices[v])));
The problem was that the vertex positions are local and so they deform around the center of their own mesh rather than around world point 0.
Excellent! It works perfectly now. Thanks again! In case someone needs to use this, in order for it to work correctly I also had to move the emptyObject to (0,0,0) and position its children accordingly.
Answer by Zumwan · Apr 28, 2014 at 03:58 AM
After much investigation and mathematical calculations I came upon the answer. I share it in case it is useful for someone else. I excecuted 3 methods after assigning each of the four points' coordineates using the aforementioned formula:
void calculateRotation()
{
transform.rotation = (new Quaternion (0, 0, Mathf.Atan ((point1.y * point1Previous.x - point1.x * point1Previous.y) / (point1.x * point1Previous.x + point1.y * point1Previous.y)),0));
}
void calculateScale()
{
transform.localScale = (new Vector3 (Vector3.Distance (point1, point2) / distScale, Vector3.Distance (point1, point3) / distScale, 1));
}
void calculateTrans()
{
transform.position = (new Vector3 (original.x + matrixFields [2], original.y + matrixFields [5],0));
}
My points are distributed the following way: point1 is in the upper left corner, point 2 on the upper right corner, 3 lower left and 4 lower right. distScale is a variable where I store the original distance between points 1 and 2 (assinged on Start, same for x and y because mine is a square object), original stores the original position of the parent object.
EDIT: After a lot of testing this doesn't work correctly. IT can't handle skewing and it sometimes reflects and rotates the object wrong. Still open to solution. Someone in the Forum suggested that I use Unity's 4x4 Matrix. However, I don't know how to do it. Thanks!
You could probably do this with the $$anonymous$$atrix4x4 class but it might be overkill if you only want a 2D solution, and maybe harder to work out the rotations you want etc, I will post a $$anonymous$$atrix3x3 class in a second once I have created some examples of use.
4x4 matrix works just fine with 2D as well, just leave z component to zero. You could manually update only the 3x3 area and leave the rest as-is
Answer by joel_cambrian · Jan 24, 2019 at 07:00 AM
Look at the source code for OpenCV getPerspectiveTransform.
Your answer