- Home /
Calculating an angle to rotate some tangent around an axis
I don't even know how to Google my question to find an answer so I drew a picture, below. I have a weapon who's Field of Fire I'm trying to rotate so a target comes into view.
I've previously been calculating Theta (below) from my weapon's exit aperture and rotating my parent GameObject by that angle, Theta.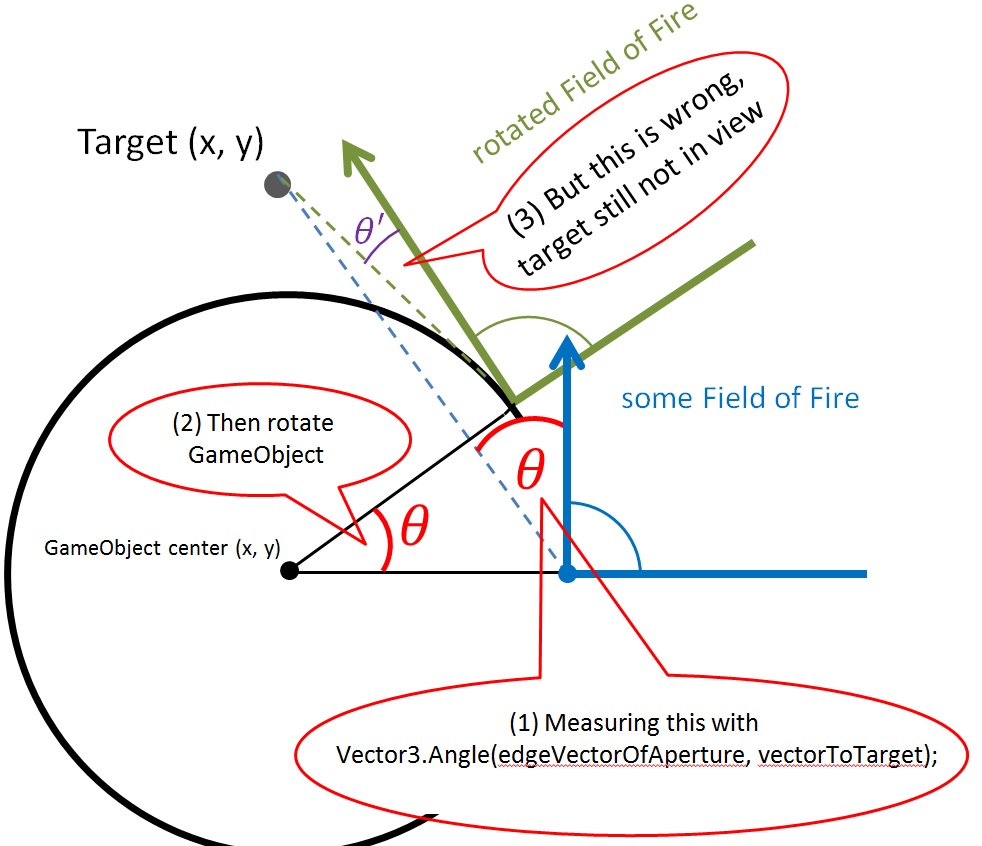
After drawing it out, I now understand that's not enough since my exit aperture is on the outside radius of (what is effectively) a circle and I always end up with some "error" Theta' (prime).
I would love a math wiz to help me calculate the angle my circle needs to rotate in order for a target to come into my field of view. My domain is 2D - everything is on the same y-plane. The center of the circle, target (x,y), radius, exit aperture (x,y) and min/max directions are all known.
ok you have the exitAperture, which I'll assume is your starting angle/vector. And you have your target vector. To find the angle between these two vectors you can use the Vector2.Angle function (https://docs.unity3d.com/ScriptReference/Vector2.Angle.html)
angleBetweenApetureAndTarget = Vector2.Angle(exitApertureVector, targetVector)
Is this what you were looking for?
Not quite. I'm using that now which gives me angle Theta in the drawing. And that would work if I were pivoting at the exitAperture. But I'm pivoting at some other point r (radius) units away, leaving me the problem illustrated above.
Ah- I was assu$$anonymous$$g center was (0,0,0) So, it sounds like you want to know the angle between:
(exitApertureVector - center) (vector from center to exit aperture)
and
(targetVector - center) (vector from center to target)
Note, when center IS (0,0,0), we have the same results I assumed earlier.
OR, are you are looking for the angle between: the vector from aperture to target: targetVector - exitApertureVector and the vector from center to aperture: exitApertureVector - center (from your drawing it looks like this one is what you want, but I don't see why. I don't think this is the right angle to rotate the circle to make the aperture point at the target.)
I’m kinda lost, no clue what’s happening in the image above, but from the sound of it you are trying to find the $$anonymous$$imum angle a object (weapon) should rotate so that a point, previously out of it’s FOV, is visible. Am I correct?
Lordlycastle you are exactly correct.
Glurth, your first scenario is close (exitA - center to target - center), except I want the $$anonymous$$imum angle I need to rotate, as lordly points out.
Answer by Glurth · Mar 29, 2015 at 08:06 PM
Ah, that clears things up a bit!
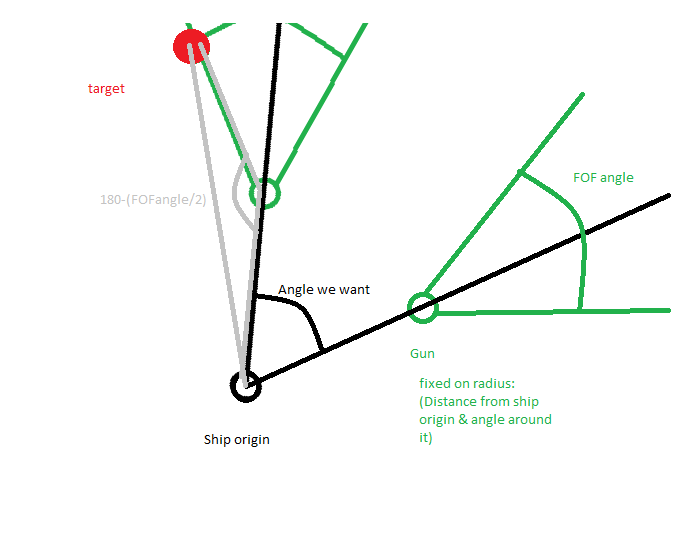
consider the grey triangle: if we can solve for that bottom angle we can simply use angle addition/subtraction to get how far to rotate.
For the grey triangle we have:
the leftmost side has length of (target-center).magnitude
the lower right side has length of the (gunsposition-center).magnitude
we also have one angle for the triangle, a constant variation on the FOF angle: 180-(FOF/2)
With this information we should be able to solve the triangle completely. http://www.mathsisfun.com/algebra/trig-solving-ssa-triangles.html
You should only need the first step though, using the law of sines: I got...
TopAngle = ArcSin( Sin(180-FOF/2)*(gun-center).magnitude/(target-center).magnitude )
BottomAngle = 180-(TopAngle+(180-FoF/2)); //angles add up to 180 for triangles
Thanks again! Your picture didn't come through on this post...
Hmm, I see the picture, in the answer, looks ok- anyone else having trouble seeing it?
Your answer

