- Home /
Finding volume of two 3D meshes intersection.
Hi, in my particular case I wan't to find out the volume of a simple cube (or other primitive) partially "merged" with a complex mesh of undefined complexity, although convex; I want to subtract the intersection to the cube to find out its remaining volume. Furthermore, this needs to run on phones and in realtime; but I don't really need an exact calculation (although the error margin can not be huge).
I've been looking into boolean operations, but the fact that the mesh is not made out of primitives and that I need to rely on plugins to operate in unity makes me feel that there must be something else.
Example of my basic case as seed from a side view, I wan't to find out the inside volume of the cube: 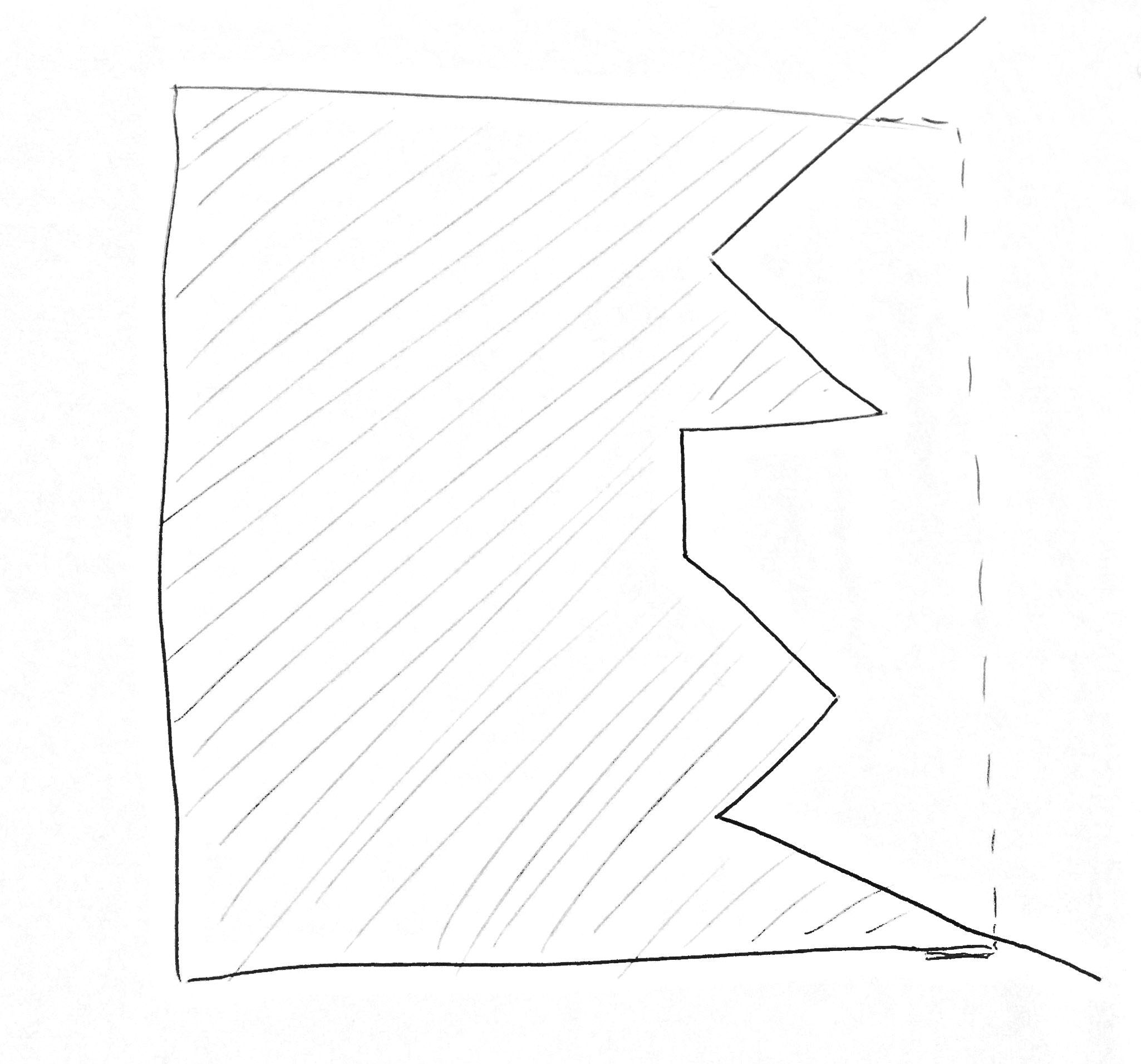
I'm interested in this question too. What plugins did you find?
Hi, I'm afraid I found no plugin that solved my issue. I couldn't come up with an efficient way of solving this either. If you are not so concerned as me for efficiency you could try finding the mesh vertexes inside the area (that's easy) and then preserve the already existing triangles in it and create new ones, a triangle strip like algorithm probably works just fine; with this it only remains to invert normals and generate a new mesh that combines both previous one, a simple built in mesh.combinemeshes might work. This, however, seems too much work for a task this simple.
What I did and thus can say definetely works is to simplify the problem, I realized that I didn't need a precise value for my volume, an aproximation that never underestimates will suffice. To get this I did use boxcast to find the lowest point of the mesh below my cube. With that and knowing the relative position of the cube to the mesh it comes down to a simple cross-multiplication to find out the ceiling of the volume. Im sure that taking this route and doing a couple more boxcasts (or raycasts) you can approximate a value good enough for most cases.
I'm making a PC game, where an operation like this will run probably 2 times a frame.
What I was looking for is a way to see if this box is over half way into the ground, and then pushing the player up enough to be half way in. I don't care about the other sides of the box being filled, just what's underneath
How would you get the points of the mesh inside the box? That, along with 4 raytraces for each corner, seems like it would be enough.
$$anonymous$$nowing whether a mesh point is inside or not of the cube might be tricky. Can you reasonably go through all the candidate vertexes? (if your mesh is either simple or subdivided into a bunch of simpler meshes this could be feasible), given some points finding wether they are or not inside the cube could be solved with a raycast for each of them.
Answer by Bunny83 · May 23, 2016 at 11:15 AM
Yes, this is a quite difficult problem to solve. I doubt there are any reliable approximation methods which always work. The usual straight forward approach would involve some advanced algorithms:
First you need to clip your mesh so the resulting mesh only contains the "wanted" volume. This first step is the most complicated. You basically need a CSG intersect algorithm which can create a new mesh out of the intersection of two (boolean operation). You should clip the more complex mesh on the simple mesh. So all triangles of the complex mesh outside the simple mesh are ignored. The triangles which intersect the simple mesh need to be clipped. So new vertices need to be calculated and new triangle faces created.
Once you have your final mesh You might want to test if the mesh is a convex or concave mesh. If it's concave you need to split it into several convex meshes.
Once you have only convex volume meshes you can simply pick the center of each sub mesh and treat each triangle of the mesh as a tetrahedron. This does only work with convex meshes. The sum of those tje volumes of all those tetrahedrons is your wanted volume.
To calculate the volume of a tetrahedron you just need to use the tripple product and divide by 6. The link that Eno Khaon posted above also uses the tripple product, but calculates it "manually".
The tripple procuct in Unity would look like this, given the 4 corner points of our tetrahedron:
public static float CalcVolumeTetrahedron(Vector3 p0, Vector3 p1,Vector3 p2,Vector3 p3)
{
Vector3 a = p1-p0;
Vector3 b = p2-p0;
Vector3 c = p3-p0;
return Mathf.Abs(Vector3.Dot(Vector3.Cross(a,b),c) / 6f);
}
The Mathf.Abs is needed, otherwise the volume could be negative depending on the order of the vertices.
I don't think there's a simpler way to do this.
One very rough approximation would be to create a voxel grid around your mesh and do a "contains check". This however can be a bit tricky for concave meshes so you might want to split the complex mesh into several convex meshes. So you would have to check every point inside the simple mesh if it's inside of any of the convex meshes. Finally just count those which are inside and divide by the total number of voxels inside the simple mesh. The smaller your voxel grid is the better the approximation but the computational complexity increases by the power of 3.
A point is inside a convex mesh if the point is behind all planes that each triangle create. Unity's Plane struct might be helpful here.
Can't you calculate the volume through the area of one of the sides and the average height of the ones above? So, to calculate the volume of a pyramid with points (<0,0,0>,,,,) you could use ((E+F)|AD-BC|)/12 ? I think I'm co$$anonymous$$g up with a solution right now, that seems simpler.
I'm not sure what "E" and "F" should be in your formula as a tetrahedron has only 4 vertices 6 edges and 4 faces.
The tripple product does exactly what you said in your comment. The magnitude of the cross product between two vectors is equal to the area of the parallelogram that those vectors define. Half of that area is the area of the base triangle. The height of the tetrahedron can't be calculated that easy from the length of the edges without some trig or "Pythagoras".
However since the vector that is returned from the cross product is perpendicular to the base, we just have to project one of the edges to the top vertex onto that normal vector to get the height. Since the length of the "normal vector" is already equal to the area of the base, the result is the volume of the "parallelepiped" defined by those 3 vectors. The volume of the tetrahedron with the same 3 vectors has 1/6 the volume as the "parallelepiped".
However as i said the main problem is not to calculate the volume of those simple shapes, but the process to break it down into those.
I meant a pyramid with a one 4 sided part.
And, I am currently working on a solution to cutting up into those shapes in python, then to convert it into C# for use in unity.
I will post the python solution when I have it
Also, note, I am working with a special case where my intersector is a box, and I only care about it being filled from the bottom.
This is basically what I concluded myself, the issue here resides in the Boolean operation, for which I found no working built in solution. And I'm pretty sure that implementing Boolean Operations to solve the issue might be overkill.
That being said, if no other alternative is proposed I'll accept this as the answer in a while; but I still would love to find a working solution, not for me (since I evaded the problem) but for future generations.
Your answer