- Home /
Finding a specific point on the edge of a triangle
Hello everyone! So, we have a triangle composed by points a, b, and c in 3D space. The point we are trying to find is point p and it is on the line segment between a and b. However, the one other defining characteristic of point p is that the line segment it creates with point c is perpendicular to a and b. Please take a look at the attached picture for greater clarity.
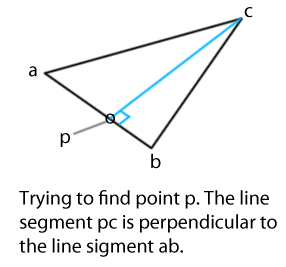
A solution I can't seem to see through was to get the plane's normal (n1) by cross product ca with cb.
n1 = ca cross cb
Then, cross product this normal with ab to get all vectors that are perpendicular to ab (including pc).
n2 = n1 cross ab
Because pc is parallel to n2, it would seem that the vector n2 could be a key to solving this puzzle. Additionally, the dot product of n2 and pc would be the positive or negative magnitude of both vectors multiplied together.
n2 dot pc = (+/-)(magnitude of n2)(magnitude of pc)
Also, when we dot product pc with n1, the result should also be zero (because pc is perpendicular to n1):
n1 dot pc = 0
I'm pretty sure both of the dot products are instrumental in finding out the x, y, and z values of p. Maybe another solution would simply be by setting the line pc equal to the line ab. Or, a combination of setting the lines equal to each-other (getting the intersection point) and these cross/dot product identities. Can someone help me out here and remind me how to do this?
Thanks for your time and help!
Couldn't you try the following approach:
You have the coordinates of a, b and c in 3D space. Run a loop that checks every point on the vector ab going from a to b, and for each point, check the angle between the vector ab and the vector pc with p the current point you're checking. If the angle is 90 degrees, stop the loop and return the 3D coordinates of point p. Of course checking every point between a and b is impossible since there are infinite points so you might have to use a threshold, let's say move every point p with 0.01f each time and check if the angle is between 89.9 and 90.1 degrees. I hope this helps you out a bit
Hey $$anonymous$$, I posted this same question on stack exchange as well and got the perfect answer over there. Your answer would be a good one to save time if there weren't a better answer. It turns out that point p is simply the projection of ac onto ab! And there is a function in Unity that actually does projections. So, I will update this post with an answer. Thank you for your response, however!
Awesome! I didn't know about that function so thank you for sharing. Good luck with your project!
yep, thank you, i know that function, i was try some example, but it worked dont like i was expect :(
Answer by slammin · Jan 05, 2017 at 07:01 AM
This is the answer -- which I got from stack exchange after I posted this question there too.
It turns out that point p is the projection of ac onto ab! And, there is a projection function in Unity that solves this problem marvelously. So:
1) add the projection of ac onto ab to point a

Your answer