Calculate UV coordinates of 3D point on plane of mesh's triangle

Interpolation in a 3D triangle is relatively easy: for any given point inside the triangle, we can find 3 interpolation factors that work as weights - we multiply the values associated to the vertices by their corresponding interpolation factors and add everything together. In the case mentioned in your question, for instance, we could find factors a, b and c for a given point P, and calculate the UV pair at this point as:

 var uv: Vector2 = a * uvA + b * uvB + c * uvC;

where uvA, uvB and uvC are the uv pairs associated to vertices A, B and C.
These interpolation factors are called the barycentric coordinates of the point, and can be calculated according to the drawing below:

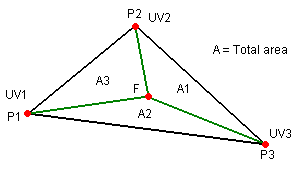
The vertices here are P1, P2 and P3, and the point is F. We can think of F as a 4th vertex that divides the main triangle in 3 smaller ones: the areas of these triangles are proportional to the factors we want - the factor a1 (associated to P1) is given by A1/A, a2 = A2/A, a3 = A3/A.
In order to calculate these areas, we use (guess what?) cross products: the cross product of two vectors has a magnitude equal to twice the area of the triangle formed by the two vectors. For points inside the triangle, we can simply get the magnitude of the cross products - it's twice the actual area, but this makes no difference because we're interested solely in the ratio between areas:

 // calculate vectors from point f to vertices p1, p2 and p3:
 var f1 = p1-f;
 var f2 = p2-f;
 var f3 = p3-f;
 // calculate the areas and factors (order of parameters doesn't matter):
 var a: float = Vector3.Cross(p1-p2, p1-p3).magnitude; // main triangle area a
 var a1: float = Vector3.Cross(f2, f3).magnitude / a; // p1's triangle area / a
 var a2: float = Vector3.Cross(f3, f1).magnitude / a; // p2's triangle area / a 
 var a3: float = Vector3.Cross(f1, f2).magnitude / a; // p3's triangle area / a
 // find the uv corresponding to point f (uv1/uv2/uv3 are associated to p1/p2/p3):
 var uv: Vector2 = uv1 * a1 + uv2 * a2 + uv3 * a3;

Notice that this works only for points inside the triangle - but normally this isn't a limitation, because points outside the triangle in UV space usually are meaningless: they can be in a blank area or inside another triangle with a completely different shape.
Anyway, if you really need to interpolate (extrapolate?) points outside the triangle, a more general approach must be used: the "sign" of each area must be taken into account, which produces correct results for points inside or outside the triangle. In order to calculate the area "signs", we can use (guess what?) dot products - like this:

 // calculate vectors from point f to vertices p1, p2 and p3:
 var f1 = p1-f;
 var f2 = p2-f;
 var f3 = p3-f;
 // calculate the areas (parameters order is essential in this case):
 var va: Vector3 = Vector3.Cross(p1-p2, p1-p3); // main triangle cross product
 var va1: Vector3 = Vector3.Cross(f2, f3); // p1's triangle cross product
 var va2: Vector3 = Vector3.Cross(f3, f1); // p2's triangle cross product
 var va3: Vector3 = Vector3.Cross(f1, f2); // p3's triangle cross product
 var a: float = va.magnitude; // main triangle area
 // calculate barycentric coordinates with sign:
 var a1: float = va1.magnitude/a * Mathf.Sign(Vector3.Dot(va, va1));
 var a2: float = va2.magnitude/a * Mathf.Sign(Vector3.Dot(va, va2));
 var a3: float = va3.magnitude/a * Mathf.Sign(Vector3.Dot(va, va3));
 // find the uv corresponding to point f (uv1/uv2/uv3 are associated to p1/p2/p3):
 var uv: Vector2 = uv1 * a1 + uv2 * a2 + uv3 * a3;

NOTE: Once you have the barycentric coordinates (or interpolation factors), any values associated to the vertices can be interpolated exactly the same way: colors, normals, depth, custom values, whatever. This is extensively used in shaders: the values passed in the output structure from the vertex function to the fragment function are interpolated by the GPU much like above, so that the values each fragment actually receives in its input structure vary according to the fragment position in the triangle.