- Home /
Radius of a Non-Uniform Sphereoid/Ellipsoid at a Given Surface Point?
Hello!
I have spent a few days mulling over this problem, but have made little progress. Unfortunately, spherical trigonometry is not my strong point. I hope you can help!
What I require is a function that given an input vector, will return the radius of a sphereoid at the point where the vector would intercept the spheroid's surface, assuming assuming that the given vector extends from the sphereoid's center.
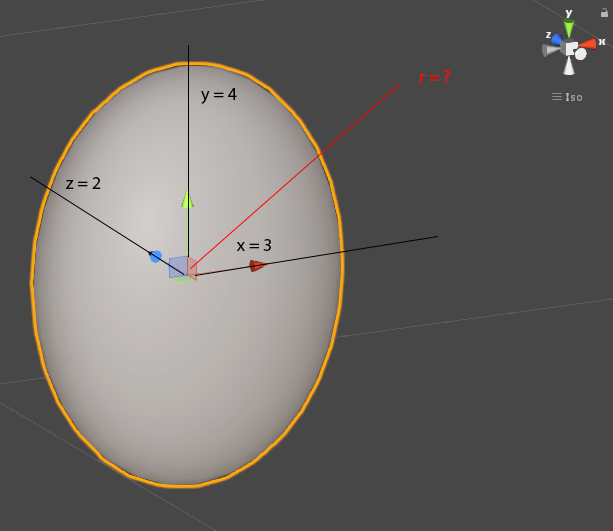
I've explored numerous equations, but most only handle elliptical radii (and I struggle to combine the third direction), or give me results that fluctuate as the input vector is modified.
Any assistance is greatly appreciated! :)
Thank you and be well!
-S.
Answer by Bunny83 · Dec 11, 2016 at 05:25 PM
Well, the easiest way is to treat the ellipsoid as a stretched spherical space. So all you have to do is un-stretching your vector, normalize it and stretch it back
// untested
Vector3 ProjectOnEllipsoid(Vector3 aEllipsoidSize, Vector3 aDir)
{
aDir.x /= aEllipsoidSize.x;
aDir.y /= aEllipsoidSize.y;
aDir.z /= aEllipsoidSize.z;
aDir.Normalize();
return Vector3.Scale(aDir, aEllipsoidSize);
}
Unfortunately there's no easy way to divide two vectors component-wise in one operation so you have to do it manually.
$$anonymous$$eep in $$anonymous$$d that when you actually used the default sphere that the radius is actually 0.5 and not 1. So when you scale the gameobject to ( 3, 4, 2 ) the actual radii would be (1.5, 2, 1). Also if you actually use a stretched default sphere you could simply do:
dir = (transform.worldToLocal$$anonymous$$atrix * dir).normalized*0.5f;
return transform.localToWorld$$anonymous$$atrix *dir;
Note: TransformDirection / InverseTransformDirection does not take the scale into account so they can't be used. However using the world to local and local to world matrices should work just fine since the vector3 is implicitly converted into a vector4 and w defaults to 0, so it doesn't apply the translation but only rotation and scale.
Both of these solutions do in fact project a point on a sphereoid (with the first example merely requiring the additional conversion from scale to radius).
Technically my question was how to obtain the radius, so the answer would be to take either solution and wrap the return with ().magnitude;.
Uhm, that should be pretty obvious ^^. In most cases the actual vector to the intersection point is much more useful than just the length of radius at that point. Technically that vector is the radius (it's the line that connects the center with the perimeter / hull).
Understood! Just wasn't certain how explicit to be for future readers.
Thank you so much for your help! Your solution(s) are elegant, and they certainly saved me many more hours of pondering. :)
Your answer