- Home /
Angle between two rotation axis-vectors (illustration inside)
Hello all,
I have a problem for which I wasn't able to find a solution by myself for now because i have too less experience in Unity3D and rotation matrices. Several attempts did not work and so i hope someone of you has an answer or an idea.
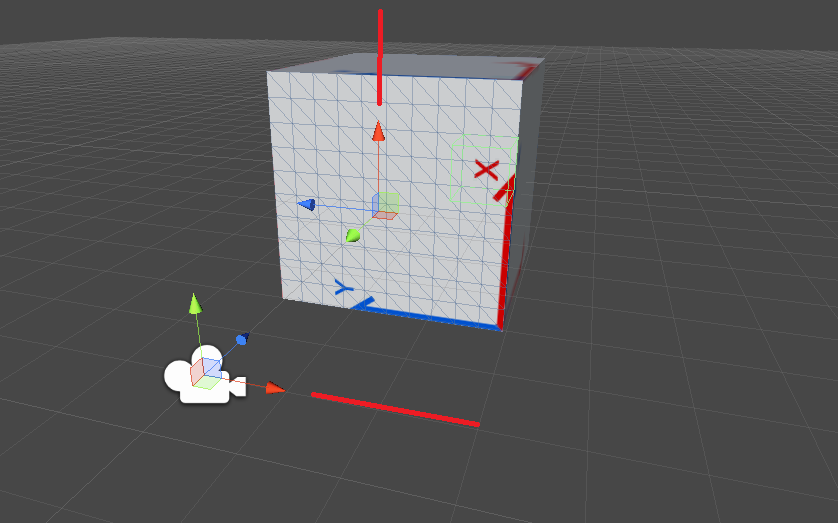
I have a cube and a camera which is pointed on a single side of the cube, as you can see on the pictures below. The local coordinate system of each side is always the same as the texture on the panel. When i move the camera to the left side, as in the 2nd picture, the red axis of the camera is not aligned in the same way as the the red axis of the coordinate system of the new side. But to know how I have to rotate the camera in the next step, I have to know how are the two objects are standing to each other based on the rotation of the red axis of the objects. (Like two vectors reproduced on a circle)
1st pic:
The red axis of the camera is 0 degrees different to the panel.
2nd pic:
The red axis of the camera is +90 degrees different to the panel.
3th possible situation:
The red axis of the camera is -90 / +270 degrees different to the panel.
4th possible situation:
The red axis of the camera is -180 / +180 degrees different to the panel.
But i have no idea how to get these values out of the transform.rotation of the two objects. Maybe there is a simple solution, but i can't see it by myself now.

Answer by doctorseus · Aug 27, 2013 at 03:50 PM
I solved the problem by myself, but maybe someone will also need the answer in the feature.
I ended up by using the transform.right vector of the camera and the side. To know if a angle of 90 degrees is -90 or +90 degrees i used the cross vector of the camera. Don't forget to move the camera rotation into the local coordinate system of the side.
float angle = Vector3.Angle (side.transform.right, camera.transform.right);
if (angle == 0) {
//Camera 0 degrees
} else if (angle == 90) {
Vector3 crossVector = Vector3.Cross (
side.transform.InverseTransformDirection(camera.transform.forward),
side.transform.InverseTransformDirection(camera.transform.up)
);
if (crossVector.z > 0) {
//Camera +90 degrees
} else if (crossVector.z < 0) {
//Camera -90 degrees
}
} else if (angle == 180) {
//Camera 180 degrees
}
Thanks robertbu for you answer and the hint with Quaternion.FromToRotation. My problem was that i simply did not know transform.right, transform.up or transform.forward.
Answer by robertbu · Aug 25, 2013 at 12:04 AM
I'm a little fuzzy about what exactly you are asking. But I'm going to take a shot at an answer. So we have a cube. If we put a texture on each side of the cube, that texture would face different directions. We can define those directions locally. For example if you wanted locally the 'up' for the texture for each of the six sides of a cube might be:
Front - Vector3.up
Back - Vector3.down
Right - Vector3.up
Left - Vector3.up
top - Vector3.back
bottom = Vector3.forward
So if any side is facing the camera (or is parallel to the plane of the camera), we can calculate the up vector by using Transform.TranslateDirection(). Let's say the 'top' was facing the camera, we could rotate the camera so that it's orientation matched the texture orientation by:
var toMatch = cube.transform.TransformDirection(Vector3.back);
var upInRotate = cube.transform.TransformDirection(Vector3.up);
var deltaRotation = Quaternion.FromToRotation(Camera.main.transform.up, toMatch, upInRotate);
Camera.main.transform.rotation = deltaRotation * Camera.main.transform.Rotation;
To do the other sides, substitute the vector from the list above into the first line of code, and the side facing the camera into the second. Likely you will want to build an array of vectors.
Hello robertbu, thank you for your answer. It was not exactly what i searched for but i looked through your posted code and the idea of the vectors and the docs of FromToRotation gave me a good start for a new try. I think the vector transform.right is exactly what i am looking for. I will try to use it to calculate the angle. Thank you very much for your idea.
Your answer