Correct use of SignedAngle?
I'm trying to get the angle between two vectors from the perspective of a plane. Sounds like exactly what SignedAngle(Vector3 from, Vector3 to, Vector3 axis) is supposed to do. However i'm not getting the result that i want and now i want to know if i don't use the function correctly, if the function is not doing what i think it is, or if it is just plainly a bug.
In short: if i move one vector parallel to the "axis" the returned angle also changes, even though viewed from "axis" the moved vector only differs in length to that perspective, not in angle..
Long story: I have 3 Nodes, A parent, the current Node, and a child. I'm trying to get the roll angle between the parent orientation (so the parents up vector) and the direction of the child.
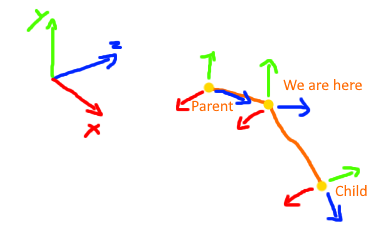
So what i do is "look at the scene" from the parent's forward vector and determine the angle between the parents up vector and the direction vector of the child.
In code:
Vector3 parentForward = parent.transform.TransformDirection(Vector3.forward);
Vector3 parentUp = parent.transform.TransformDirection(Vector3.up);
Vector3 childDirection = (child.transform.position - current.transform.position).normalized;
float roll = Vector3.SignedAngle(parentUp, childDirection, parentForward);
If i now rotate the child around the parent on the global x axis (parents z axis) everything works as intended, as seen in the left image of the following illustration (viewed from the front = global -x axis).
If i however rotate the child in the global z axis (parents -x axis) the angle also gradually decreases, as if i had just rotated it for the same amount on the global x axis (right image, viewed from behind = global z axis)
But as the given rotation Axis is the global x axis, rotating around the z axis should not have an effect on the result, at least as far as i understand it. (at least not until i overshoot the 90° where the angle between parent and child turns from 180° to 0° instantly)
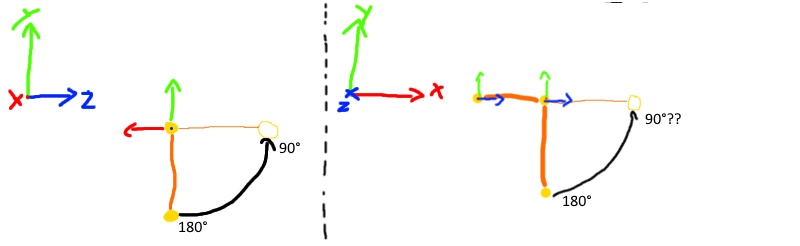
is this intended behaviour? if so, what is the parameter "axis" for?
Answer by SlaxXx · May 05, 2020 at 02:50 PM
Looking at the implementation of SignedAngle (https://github.com/Unity-Technologies/UnityCsReference/blob/master/Runtime/Export/Math/Vector3.cs) this indeed seems to be intended behaviour. The "Axis" is only for determining the sign. I will attempt to implement my wanted behaviour of calculating the angle in the perspective of a given rotational axis and hopefully get back to you with my results.
Edit: The solution to this was actually really simple:
public static float GetAngleOnAxis(this Vector3 self, Vector3 other, Vector3 axis)
{
Vector3 perpendicularSelf = Vector3.Cross(axis, self);
Vector3 perpendicularOther = Vector3.Cross(axis, other);
return Vector3.SignedAngle(perpendicularSelf, perpendicularOther, axis);
}
What i did is calculate the Cross product of the axis and both vectors. What i essentially get from that is a projection of the vector onto the "viewing-plane" of the axis. it is indeed rotated by 90° after that, but as i'm rotating both vectors by the same amount, the relative angle stays the same.
Now that both angles are projected onto the plane i actually want the angle from, i can simply use SignedAngle again to get the correct angle this time.
DISCLAIMER: I'm currently on a tight schedule so i only confirmed that it looks right in my project. It is not properly tested and might return weird values under certain circumstances. Use with caution if values have to be absolutely positively right.
Your answer

