- Home /
Finding Point on a Bounds (2D Rectangle) using its Centre and an Angle.
Sorry if this is a lame post. I cannot describe what I am trying to achieve as I lack the terms. This means Google is no good to me, so I ended up here.
I am not necessarily looking for copy and paste code. I was just wondering if someone could help me. In my side project using Unity for the first time, I managed to collect together the Bounds of all the elements I want. So I know the centre and I know an arbitrary angle from a controller for example.
I cannot figure out the next step on how to reach the Red Circle Point and would appreciate any advice.
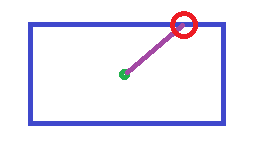
Bounds (Blue)
Bounds Centre (Green)
Any Angle (Purple)
What I need (Red) as a Vector.
Answer by Bunny83 · Jul 28, 2016 at 11:32 AM
Here i quickly wrote those two helper functions:
public static Vector2 PointOnBounds(Bounds bounds, Vector2 aDirection)
{
aDirection.Normalize();
var e = bounds.extents;
var v = aDirection;
float y = e.x * v.y / v.x;
if (Mathf.Abs(y) < e.y)
return new Vector2(e.x, y);
return new Vector2(e.y * v.x / v.y, e.y);
}
public static Vector2 PointOnBounds(Bounds bounds, float aAngle)
{
float a = aAngle * Mathf.Deg2Rad;
return PointOnBounds(bounds, new Vector2(Mathf.Cos(a), Mathf.Sin(a)));
}
Note: The used Bounds has to be in the same coordinate system as the direction vector / angle. The angle is as always counter clockwise, specified in degree and "0°" points to the right.
Collider.bounds and Renderer.bounds returns the bounds in worldspace. So the box is axis aligned to the world axes. However Mesh.bounds is defined in localspace so the direction vector has to be in localspace as well.
I haven't tested the method. The idea is to project the center along the direction first onto the "x" size of the bounds. If the resulting point is outside the bounds we do the same for the y size. So in your example image the first case would be outside the bounds. If you extend the purple line until it crosses the "x size", the y position would be above the bounds rect (somewhere below your word "step" in the text above). So the second case would apply here.
Thanks for taking the time to respond to me. I will attack this post tonight when I go home. It is 90% making sense! :)
Your answer