koobas.hobune.stream
Vector math problem
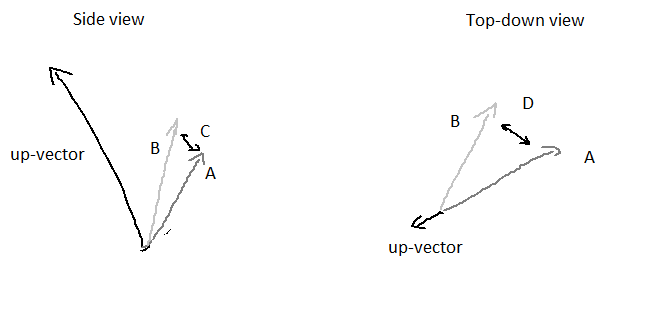
I have two vectors (a and b) and an up-vector, which can point in any direction. I need to find the distance between A and B, but only the distance from the perspective of the up-vector (D). So without the distance seen in the side view (C).
How do I do this? I don't know where to begin.
I have thought about it, but that would cause problems, because the up-vector can point in any direction.
I basically want the 2d distance, between 3d points, with the up-vector being the normal of the 2d plane.
$$anonymous$$mm, one thing you could try is to use A dot up and B dot up.
This will result in the length of the projection of A onto up and the length of the projection of B onto up. Then comparing those two length you may get what you need. Not sure though.
You can project the two points onto the plane defined by up-vector and common vertex of the three rays. You can find a script with many 3D math routines including projecting a point onto a plane here:
But which one is the answer? There are dozens of methods on the link you provide.
I'm not sure why someone converted my answer to a comment. What you want is exactly as I describe. The math script at this link contains a ProjectPointOnPlane(). The plane is defined by the up vector and the common vertex point. Project A and B onto the plane and then get the distance.
Yeah, this was exactly what I used and needed. Thanks.
