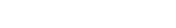Procedural circle mesh with uniform faces

This won't give you exactly as good results but this is the approach I would try (I won't code it all out here though): First, find your vertices. For that I would start at the center. Then define a mean edge length for your triangulation, let's call it "l". It defines the density of the resulting mesh. Now iteratively increase a your radius r by l until you reach your desired full circle radius. At each iteration i, determine the vertices that lie on the circle with the radius l*i. the amount of vertices at each circle should be chosen so the distance between these vertices is as close as possible to l. Once this is done, you should have a bunch of vertices with more or less equal space between them in a circular shape.

Next you will have to triangulate those vertices. I would suggest you look up Delaunay Triangulation for that. It gives the least "slithery" triangles, meaning it avoids narrow angles in your triangles, which makes it a very good triangulation for many purposes. It is so well known that you should find enough clues on how to implement it online.

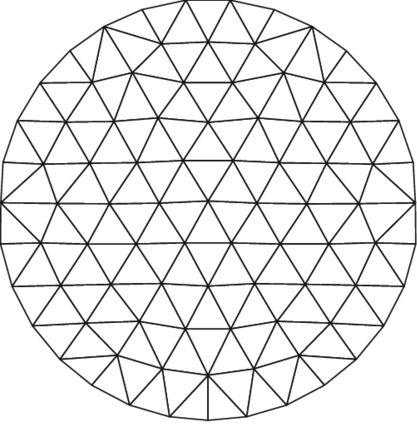
First of all if we analyse your example you get this:

As you can see it's actually not that well distributed. However you can see some generally valid geometry which can be justified just fine by looking at the numbers. The general layout is a hexagon. The center hexagon is a "classical" hexagon made up of 6 equilateral triangles with side length 1. This gives a diameter of 2 and a circumference of 6. The enclosing circle of the inner most hexagon also has radius 1 but a circumference of 2PI (6.283).

If you look at the next ring (green) it has a radius of 2 (diameter of 4) and 2 times the number of triangles. The next ring (yellow) has a radius of 3 (diameter of 6) and 3 times the number of triangles. This pattern continues. The 4 spikes in the blue ring wouldn't be necessary if we had continued the pattern in the outer ring just like at the bottom part.

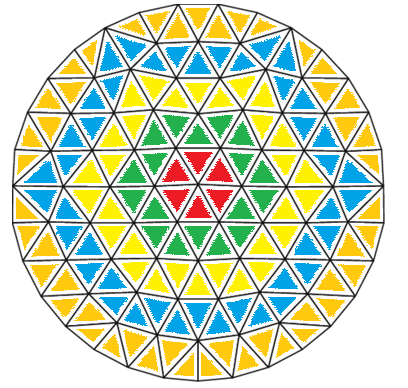
. To generate this you can look at the problem in a different way. This is the same circle colored in a different pattern:

As you can see the circle actually is nothing but a big tessellated hexagon but the further you go out the more the intermediate points are pushed outwards to it's circular equivalent. If you just create a tessellated hexagon and lerp the intermediate points between the tessellated hexagon points and the points on the corresponding point on the circle radius of each ring you get a result similar to your example. Just keep in mind that you increase the lerping from 0 to 1 as you go from the inner most ring to the outer ring. So the outer ring will bit an actual circle while the rings in between are not exactly on their circle . The orange big triangle roughly shows how it would look like. Though it has one additional triangle here.

So you have to decide how many rings you want to use. Divide your desired circle radius by the ring count and you get your "unit length" for the innermost ring / hexagon. How you create the circle points is up to you. However the easiest way would be to just divide each ring into X equal parts where X is 6*ringIndex

It's been answered on Stackoverflow. Credit to Yuri Nudelman.

 using System.Collections.Generic;
 using UnityEngine;
 
 [RequireComponent(typeof(MeshFilter))]
 public class UniformCirclePlane : MonoBehaviour {
 
     public int resolution = 4;
 
     // Use this for initialization
     void Start() {
         GetComponent<MeshFilter>().mesh = GenerateCircle(resolution);
     }
 
     // Update is called once per frame
     void Update() {
 
     }
 
     // Get the index of point number 'x' in circle number 'c'
     static int GetPointIndex(int c, int x) {
         if (c < 0) return 0; // In case of center point
         x = x % ((c + 1) * 6); // Make the point index circular
                                // Explanation: index = number of points in previous circles + central point + x
                                // hence: (0+1+2+...+c)*6+x+1 = ((c/2)*(c+1))*6+x+1 = 3*c*(c+1)+x+1
 
         return (3 * c * (c + 1) + x + 1);
     }
 
     public static Mesh GenerateCircle(int res) {
 
         float d = 1f / res;
 
         var vtc = new List<Vector3>();
         vtc.Add(Vector3.zero); // Start with only center point
         var tris = new List<int>();
 
         // First pass => build vertices
         for (int circ = 0; circ < res; ++circ) {
             float angleStep = (Mathf.PI * 2f) / ((circ + 1) * 6);
             for (int point = 0; point < (circ + 1) * 6; ++point) {
                 vtc.Add(new Vector2(
                     Mathf.Cos(angleStep * point),
                     Mathf.Sin(angleStep * point)) * d * (circ + 1));
             }
         }
 
         // Second pass => connect vertices into triangles
         for (int circ = 0; circ < res; ++circ) {
             for (int point = 0, other = 0; point < (circ + 1) * 6; ++point) {
                 if (point % (circ + 1) != 0) {
                     // Create 2 triangles
                     tris.Add(GetPointIndex(circ - 1, other + 1));
                     tris.Add(GetPointIndex(circ - 1, other));
                     tris.Add(GetPointIndex(circ, point));
                     tris.Add(GetPointIndex(circ, point));
                     tris.Add(GetPointIndex(circ, point + 1));
                     tris.Add(GetPointIndex(circ - 1, other + 1));
                     ++other;
                 } else {
                     // Create 1 inverse triange
                     tris.Add(GetPointIndex(circ, point));
                     tris.Add(GetPointIndex(circ, point + 1));
                     tris.Add(GetPointIndex(circ - 1, other));
                     // Do not move to the next point in the smaller circle
                 }
             }
         }
 
         // Create the mesh
         var m = new Mesh();
         m.SetVertices(vtc);
         m.SetTriangles(tris, 0);
         m.RecalculateNormals();
         m.UploadMeshData(true);
 
         return m;
 
     }
 }