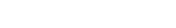What’s wrong with Vector3.normalized, or my understanding of it?
I ran into this issue when trying to normalize a small vector. At first I thought it was a precision issue, but when I tested it myself, as shown in the code below; my normalized values are computed just fine, but Vector3.Normalize just returns Vector3.zero.
I could understand some loss of precision for the sake of performance, but this result is just plain wrong. Do I really need to roll my own Vector3 TrulyNormalized(this Vector3 v) extension function? Should I submit this as a bug? OR - What am I misunderstanding / incorrectly-assuming?
I do see in the docs it explicitly states: "If this vector is too small to be normalized it will be set to zero." but I really don't know what "too small" is, nor why this should be the case.
Test code:
float x = 5E-16f;
float y = 1E-16f;
float z = 0;
float d = x / y;
float magsqd = x * x + y * y + z * z;
float mag = Mathf.Sqrt(magsqd);
string log = (" x: " + x.ToString()+ " y: " + y.ToString()+ " z: " + z.ToString()+ "\n sanity check x/y: " + d.ToString() + "\n xyz.magsqd: " + magsqd.ToString() + " xyz.mag: " + mag.ToString() );
float an = x / mag;
float bn = y / mag;
float cn = z / mag;
log += ("\n My normalized vector xn: " + an.ToString() + " yn: " + bn.ToString() + " zn: " + cn.ToString() );
Vector3 vec = new Vector3(x, y, z);
Vector3 vecNorm = vec.normalized;
log += ("\n Vector (sanity check) vx: " + vec.x.ToString() + " vy: " + vec.y.ToString() + " vz: " + vec.z.ToString());
log += ("\n Unity Normalized Vector: vxN: " + vecNorm.x.ToString() + " vyN: " + vecNorm.y.ToString() + " vzN: " + vecNorm.z.ToString());
Debug.Log(log);
OutputResults:
x: 5E-16 y: 1E-16 z: 0
sanity check x/y: 5
xyz.magsqd: 2.6E-31 xyz.mag: 5.09902E-16
My normalized vector xn: 0.9805806 yn: 0.1961161 zn: 0
Vector (sanity check) vx: 5E-16 vy: 1E-16 vz: 0
Unity Normalized Vector: vxN: 0 vyN: 0 vzN: 0
@Bunny83 I see your answer to a similar, less "precise", question here : http://answers.unity3d.com/questions/749902/normals-not-calculating-properly-for-small-polygon.html But I think I have eli$$anonymous$$ated precision as a possible cause, as shown in my test. Any thoughts?
Answer by Glurth · Jan 19, 2017 at 05:39 PM
Edit/update:
Unity defines Vector3 equality/equivilence using this class operator, https://docs.unity3d.com/ScriptReference/Vector3-operator_eq.html, which states two vectors are equal if they fall within a certain range of each other. Regardless of the purpose (optimization, help beginners, whatever…), this is now a mathematical definition.
In order to maintain the consistency of this definition, it is necessary to specifically check against it, during some operations. As an example, the normal operation will always need to check if the vector we are normalizing has a magnitude of zero, because Vector3.zero is the only invalid vector we can input, (and in order to avoid a divide by zero error). Though one CAN check the magnitude against the value 0.0f, we could equivalently express the conditional, as checking to see if the input vector is EQUAL to Vector3.zero.
So, in order to be consistent with the unity definition of vector3 equality, but avoid extra operations, the normalize function checks the magnitude directly against the defined equality range.
(Never would have seen this without Owen's help.)
Additional FP computation details, and my moaning, remain, below.
End edit:
Normalizing a Vector is a universally standard mathematical operation. It is clearly defined, the same way, in all fields of math.
Except in Unity.
Unity decided to change this universally accepted formula, such that arbitrarily "small" vectors return Vector3.zero when normalized. Apparently, this is not a bug, it's "by design". (see Eric's answer for the actual unity code.)
I have yet to get a good reason for this choice. But, since I don't trust myself enough; if I get more than let say.. 4 up-votes on this answer, and no "good reason" is provided, I WILL submit it as a bug. Please down-vote this answer if you think I’m wrong, and there is a good reason for this limit (though a detailed explanation on why, would be most appreciated.)
After much analysis, research and tests, I have concluded that the generalized claim that this is a "32 bit floating-point limitation": is simply incorrect! (Sorry Eric.) Sample code in my OP question provides a limited proof of this, code in other professional-level software projects lends weight to this argument, and a rigorous analysis of the FP operations involved confirms it. (Analysis details below).
Another possible reason provided is that this is intended to somehow help us detect inaccurate FP values. But this requires a whole bunch of assumptions about the vector being passed in to the normalize function. These assumptions turned out to be incorrect, in at LEAST one real-world case (which is how I ran across this issue).
Both explanations seem inconsistent with the rest of Unity; everywhere else in my code, it is MY duty to ensue FP accuracy. I agree with this philosophy; and ensuring FP accuracy is most certainly NOT the duty of a normalize vector function.
It seems unbelievable, but if you want a function that performs the STANDARD vector normalization function, consistently, you actually DO need to provide your own. (Easy 'nuff to do, just very surprised it's necessary.)
Some FP analysis details:
The limit applied by unity affects a Vector3 with a magnitude of less than 1e-5, which is FAR greater than where FP limits are actually hit.
The 32 FP limit is 2^-126, or approximately 1.17e-38: this is the smallest number we can represent, with maximum precision, using a 32bit-FP.
0x0080 0000 = 1.0 × 2−126 ≈ 1.175494351 × 10−38 (min normalized positive value in single precision)
This means that if we square a number (part of the normalize operation) that is smaller than (sqrt(2^-126)), or around 1.32e-19 in decimal, the result will be too small to be represented, with full accuracy, by a FP.
So, if we compared say.. 2e-19 against the original vector components, we could determine if any of them might be too small to be squared with full accuracy.
For the normalization operation, there is a safe exception we can make. We don’t mind when accuracy-loss happens to components that are only a tiny fraction of the other components. What matters, is the RELATIVE values of the vector components. In other words, if one component is “small enough” relative to another, it’s contribution is less than the least significant digit of the input vector’s magnitude. In this case, we don’t care if the smaller component loses accuracy; because its value is simply not significant enough to affect the result at all.
This “significance” is, obviously, related to the number of “significant” digits a float can store: 7.2 decimal, lets round up to 8 for worst-cases. The value at which our 2e-19 is too small to be significant, is 2e(-19 + -8) = 2e-11.
So those are our limitations, and exceptions:
Exception: If any component is greater than 2e-11, you will not lose accuracy.
Limit: Otherwise, if any component is less than 2e-19, you might lose accuracy.
Guesses on what unity is doing:
One COULD use the vector’s magnitude to check for the exception: If the vector to be normalized has a magnitude that is greater than a certain value, we KNOW, at least one component is so large that any possible loss-of-accuracy, in other components will NOT be significant. The “certain value” magnitude to check against should also be 2e-11, since 2e-11= sqrt(2e-11^2+0+0).
So perhaps, Unity is checking for the exception, and for optimization purposes, using it as the limit?
Even then, I’m still not sure where the 1e-5 comes from. The only relation I can see to this number, is that it happens to be the approximate value of the least significant digit of a 32bit-float, when using an exponent value of 0. I guess this number DOES represent the LSB value of the normalized output vector’s largest component, but the value is actually being compared against the input vector, not the output vector: so, NOT actually relevant to the computation.
IMHO it's NOT actually the job of a normalize function to check my FP accuracy, but still, I HOPE I'm wrong about this FP stuff, since it's the only possibly-valid reason I can think of for this limitation. A sample Vector3 value, that my analysis would say works with full accuracy, but actually fails to be properly processed by a standard normalize function would be the best proof I'm wrong.
Answer by Owen-Reynolds · Jan 20, 2017 at 02:20 AM
I think the trick is that Unity doesn’t want you to use their normalize built-ins: https://docs.unity3d.com/Manual/DirectionDistanceFromOneObjectToAnother.html
That seems like an obscure reference, but it really is what everyone does. You’re going to need the magnitude anyway, so just divide by it yourself.
So who uses the normalize built-ins? I think it’s new users who are somewhat math-phobic and like to see the commands (you can normalize without calling normalize? what?) The most common use is (targetPos-myPos).normalized. You’re stating with two points. If they’re that close together, Unity decided to force you to check for almost-equal.
It’s maybe a funny change, but Unity is a game engine, and it’s documented.
It’s a little like how the built-in lerp clamps to 0-1. Normal lerp functions don’t do that - everyone knows using 1.5 overshoots by 50%. I assume they added it since most new programmers use lerp for an A to B motion.
"I think the trick is that Unity doesn’t want you to use their normalize" Very interesting, and odd.
"So who uses the normalize built-ins?" This was precisely $$anonymous$$Y point too, LOL: If one needs the magnitude ONLY for the purpose of computing the normal vector; most people familiar with standard vector functions, expect the normalize function to be sufficient. Agreed it's documented: but, after normalizing vectors for so many years, I certainly didn't expect a differently operation in Unity. I never would have read up on "Vector cookbook" without your link, thought I knew 'em well enough: thanks!
"(targetPos-myPos).normalized. You’re stating with two points. If they’re that close together, Unity decided to force you to check for almost-equal." This is exactly what I was doing when I discovered this issue (though it was mesh-vertices, not positions). The two points were NOT equal, thought they were indeed close, yet I kept getting that zero normal vector result, until I rolled my own.
Guess I just don't like stuff messing with my math. probably why I rarely use https://docs.unity3d.com/ScriptReference/Vector3-operator_eq.html either.
I'd rather do all limits/truncation myself, when appropriate. I've got no problem with it being an OPTION in Vector3, but at least let me control that Vector3.$$anonymous$$Value somehow. (Or can I?)
AH-HA! If we accept this (approximate) == operator as the mathematical DEFINITION of "equal vectors"; the limit when normalizing, makes more sense because: (smallVector3toNormalize == Vector3.zero) yields "true". I think that may be the math-logic answer to my question (to maintain consistent definition of vector equality). (agree/disagree? Thanks for sending my thoughts down this track! Or perhaps this is what you were actually saying, and I just had to beat my way around the bush.)
I always forget they overloaded Vector3::==. I have a few places where I know the result will absolutely hit 000, which I test using v==Vector3.zero. I wonder if any of them stop a frame early because of the approximately?
But, agree, == approx is another example of how the API is for making games.
$$anonymous$$y modeling friends tell me two mesh verts very, very close is something to avoid. You get a long, super-skinny triangle. As the model moves, the face tends to twist as math errors shift the nearby verts.
Oh, I cannot create a second answer. $$anonymous$$ay I edit your answer (or would you) to include the "consistent math definition of ==" stuff, and "accept" it? edit: never$$anonymous$$d- just edited and accepted my own answer. Don't really like doing that, but don't think you care ;)
Answer by Eric5h5 · Jan 15, 2017 at 08:05 AM
Precision is the cause, and there's no bug. It's not about performance, but rather due to the limitations of 32-bit floating point, which isn't specific to Unity. Hence the code for Normalize is this:
public void Normalize ()
{
float num = Vector3.Magnitude (this);
if (num > 1E-05f)
{
this /= num;
}
else
{
this = Vector3.zero;
}
}
It's trivial to decompile UnityEngine.dll, so it's simple to see what it's "really" doing, except in those cases where the function wraps native code.
"rather due to the limitations of 32-bit floating point" but my example code shows this is NOT the case: I normalize a vector that has a magnitude recorded in quadrillioths..
Based on the code you posed the limitation appears to be due to an if statement, not some intrinsic limit of 32bit floating points. Perhaps I just fail to see the point of this artificially added limitation? If so, what is it?
The if statement exists because of the limitations of 32-bit floating point. It would be a good idea to familiarize yourself with them: https://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html
Alas, I've spent many many hours studying the intricacies of floating point numbers. Though I did get an "A" in that "microprocessor design" class, that WAS over 20 years ago.
Regarding your link, I went through the whole thing: but must have missed the reason for using 1e-05f. It's a pretty big article, if you could please specify what part/point in particular you think is relevant, I'll read that again.
T1: re: computing subtractions – not applicable
T2: re: computing subtractions – not applicable
T3: rounding errors – ok, better than a result of Zero.
T4: re: computing subtractions: rounding errors – ok, better than a result of Zero.
T5: addition of whole number to floats: relative precision errors- not applicable
T6: rounding errors – ok, better than a result of Zero.
T7: working with small integers is exact- not applicable
NaN, +/- inf, +/- 0: all results we can check against: (better than 1e-05)
Denormalized numbers: good examples of true floating point issues, but those occur at $$anonymous$$UCH smaller values than 1e-05 (only for values around float.epsilon*100, would this apply)
T9: re: computing subtractions – not applicable
T10: re accuracy of addition: relative precision errors- ok, better than a result of Zero.
T11 : re: computing subtractions – not applicable
T12: re: computing subtractions – not applicable
T13: addition of whole number to floats: relative precision errors- not applicable
T14: rounding errors – ok, better than a result of Zero.
T15: recovering initial number- not applicable.
Or, ins$$anonymous$$d of an explanation, show me an actual vector value that will give a "normalize" result that is "more wrong" than a result of Vector3.zero, when using 0.0f rather than 1E-05f, in that code you posted. This would shut me RIGHT UP!
The issue is how much you trust the numbers in your very small vector. In a real, running program, your tiny test vector would have been created over time, so have lots of accumulated "rounding error." It's essentially (0,0,0) with a rounding error, which means normalizing it gives pretty much a random direction.
Unity having normalized return 000 is a way to tell you "numbers this small are so unreliable, the code calling this should be checking for the almost-zero special case, so I'll force you to do it ins$$anonymous$$d of returning a value I suspect will be wrong."
Now, 1.0E-05 is probably vastly larger than any real accumulated imprecision (but if you're moving around at x=10,000, maybe not.) But it's also much smaller than anything you'd really be using.
Wait a sec... Because I "might" have generated the vector a certain way, unity "assumes" I generated it that way? And, because that way "might" generate inaccuracy, unity "assumes" it generated inaccuracy? Is this a hypothesis or are you sure about that Owen? Seem like an awful lot of assumptions.
Of course, moving around at a velocity of 1e-10, while at position 1e+10, could very well lead to no change in position, but that is a substantially different operation from normalizing a vector.
Consider the vector (1e+10, 1e-10, 0) : inaccuracies will lead this to normalize to (1,1E-20,0) because when we compute the magnitude, the y^2 part will be rounded off when added to the x^2 part. This is NOT a problem, specifically BECAUSE we are then normalizing it.
Note: it is the difference between the exponent component of the coordinates, that creates this floating point error (normalized.x equal to 1.0f, rather than slightly less than 1), NOT the actual exponents used. The same exact rounding error and normalize result would/should occur with (1e+20,1e+0,0) AND (1e-06,1E-26,0). The actual magnitude is irrelevant.
I must grant that the true magnitude of (normalize(1e+10,1e-10,0))= (1,1e-20,0) is not truly EXACTLY 1.0, but that IS the floating point value you'll get if you compute it (Again, the same floating point rounding mentioned above, that's due to the difference in the coordinate's exponents; something I can understand, and deal with.)
@Owen-Reynolds & @Eric5h5 you guys have my greatest respect, and thanks! Not going to roll-over on this one 'till I understand it tho :)
No, the whole point of floating point is that you can handle very small or very large numbers without problems. There is no such thing as "numbers this small are unreliable".That really is not a thing, unless you get so small as more than 37 zeros after the decimal point before the first significant digit, something like:
0.0000000000000000000000000000000000001
Did you actually try that? Because it won't work with floats. I don't think you understand the difference between floats and doubles.
var num1 = 0.0000000000000000000000000000000000000000000001f;
var num2 = 0.0f;
Debug.Log (num1 == num2);
// Prints "true"...the numbers are functionally the same due to 32-bit float limitations
Interestingly: I looked up the OpenGL's version of normalize as a sanity check. It' double, rather than single floating point values, but similar principles apply. This code checks against zero, rather than some non-zero constant.
static void Normalize( GLdouble v[3] )
{
GLdouble len = v[0]*v[0] + v[1]*v[1] + v[2]*v[2];
assert( len > 0 );
len = sqrt( len );
v[0] /= len;
v[1] /= len;
v[2] /= len;
}
This is correct, because the only case of an error is when len is zero. There is no need to check against an epsilon.
You are absolutely correct in your analysis, and Unity's implementation of the normalize function is absolutely unwise and has probably been responsible for countless weird bugs.
This comment is incorrect. There is no need for the check, unless one wishes to prohibit divide by zero, but in that case one can simply check for num being non zero.
It should be possible to normalise vectors that are extremely small. This is automatically handled by floating point. You can easily normalise the following vector without problems, for example:
( 0.000000000000001, 0.000000000000000001,0.0000000001 )
Floating point calculations only have accuracy problems with the number of significant digits (approximately 6 is the limit). The above vector has one significant digit for each coordinate.
The impact of this bug (and it is a bug, even if there is an attempt to justify it) is that, as an example, you cannot normalise the result of a cross product used to calculate the normal to a triangle that is, for example, about 1-2 mm in size.
The result of the cross product is a vector that is much smaller than the Normalize function's epsilon value. In order to work around this, one must scale up the vector before normalizing it (absurd) or normalizing the vectors before the cross product (inefficient).
Sorry to say it, but it is a clear and unfortunate mistake, and since discovering it in my project today, I am looking to avoid ever using Normalize and normalized again. It's just nuts.
Answer by yawmoo · Nov 03, 2019 at 06:03 PM
Try to find the length of vector (3.0e-25f, 4.0e-25f,0.0f) which is expected to be 5.0e-25f.
Now that’s an example of vector that cannot be normalised the usual way.
The usual formula returns a length of zero.
It's a fundamental issue with floating point.
Let me explain a bit more: there are non zero vectors that can return a length of zero. This is due to the fact that floating point numbers have limited precision.
We can try using doubles which are more precise. Cool. Then the same problems appears at a smaller scale. We did not get rid of the problem, we just made it smaller.
To get rid of the problem, we could think of floating points whose precision can increase arbitrarily. But increasing the precision arbitrarily means to increase the time it takes to compute arbitrarily and that in practice means dropping frames if you hit the wrong case.
I think that what unity did was just pragmatic: If you know what you are doing it's documented and you can roll your own solutions instead of using theirs. On the other hand you are not going to fully get rid of the problem, so let's just choose a limit and everything below that is just zero so you save a few headaches and in most cases it won't be a problem as a few digits of precision are ok in a lot of cases. Choosing a higher limit than the actual limit for floating point numbers is also a pragmatic choice: recursion makes precision errors explode.
To me it makes sense. I am not saying that I would do the same if I were to write a vector library but at least it does not seem too strange to me.
Unless you have objects at very different scales in the same scene you can forget about this issue for the most part.
Problem is that for example in VR you can have a room with a very tiny object and a very big one. and you may be looking outside a window and see even bigger objects. Or you can have objects that move by a very small distance per second.
In those cases you have to be aware of the problem and roll your own solution. I don't think that there is a known and accepted solution that works in every single possible case exactly because floating point numbers don't behave exactly the same as real numbers and on the other hand people generally expect floating points to behave the same.
Not sure how you got there... The following code will return a result of (0.6,0.8,0), for that input: public static Vector3 NormalizePrecise(this Vector3 v) { float mag = v.magnitude; if (mag == 0) return Vector3.zero; return (v /mag); }
You sure you are using the exact same vector I wrote? If I do:
Vector3 v = new Vector3(3.0e-25f, 4.0e-25f,0.0f);
Debug.Log(v.magnitude);
I get a magnitude of zero printed to the console.
I expanded a little bit on my previous answer :-)
This is quite interesting. If you look at the source code, you will see that the magnitude function uses $$anonymous$$ath.Sqrt and that takes a double!
I think (because it's a little hard to decipher the C# docs) that as the function takes a double, the float multiplies are promoted to doubles. It is for this reason the example you give works.
So the whole situation is even more funny. Not only is there a totally unnecessary and intrusive clamp on the $$anonymous$$imum values, but the sqrt function is using doubles, so in fact can handle the whole float range without problems. Additionally, the use of doubles inside the magnitude function is potentially slower as the compiler has to cast back and forth from doubles.
Yes it is very strange, and very very wrong. wags finger
Take a look at this and all will become clear. And please note that even if we accept what you are saying the limit would be approx. 1E-18, not 1E-5. The documentation states that the function returns zero if it cannot be normalised, but it turns out that regardless vectors can be normalised as far as 1E-18, but they are 'clamped' at 1E-5, or 100th of a millimeter. There is no excuse for this. None. Nada. No Go.
On my test, the actual limit is about 1E-37, because the magnitude function internally uses doubles! This just adds insult to injury.
Here is a full example that should settle this argument once and for all. Read it and weep. I am.
BTW I know mistakes happen in software all the time, my beef here is any pretending that it is not a mistake. It is. 100%. I put all of my 40 years experience on this one. I am ALL IN. ;)
I don't seem to be able to upload my screenshot. Tried with both Firefox and Safari on the $$anonymous$$ac.
Point is, I get a slightly different output than yours. v.magnitude is 0 on my machine, not 5E-25. $$anonymous$$y version of unity is 2018.3.8f1 and I am on a $$anonymous$$ac.
Regarding "my beef here is any pretending that it is not a mistake", I don't think that people here are "pretending that it is not a mistake" or not. Certainly I am not even thinking in terms of "is that a mistake or not?" personally. I am just saying please consider that there might be other reasons why it's done like that.
It's a fact that after reading some linear algebra you expect an operation like Normalize never to return a zero vector and that the length of a non zero vector should not be zero.
It is another fact that floating point numbers don't behave the way real numbers behave. They do mostly but not exactly. And you will always have some edge cases where they don't.
To investigate a little further, try this on your machine ( results may be different from $$anonymous$$e as before ):
float f = v.x*v.x + v.y*v.y + v.z*v.z;
float sf = (float)System.$$anonymous$$ath.Sqrt(f);
Vector3 n = v / sf;
I hope I haven't made any gross mistake here but this should be pretty much the same as your last example, apart from splitting the calculation into different variables. It's not the same. On my machine your example shows (0.6,0.8,0.0) and this shows (Infinity, Infinity, NaN).
This is one example of the kinds of reasons why people who write that kind of code make such compromises.
What I said about avoiding headaches to beginners is about something like the following: for the most part, you want to be able to split a calculation into multiple variables to simplify it. And if you get such big differences in the results then it is a huge problem, especially as a beginner.
I know precisely because when I started doing vector maths on the computer I had these kinds of problems to deal with all the time and had to figure out what the problem was.
Yes, but I have just shown that there is no problem with normalising vectors shorter than the epsilon; that the current normalise function causes errors in otherwise perfectly valid code; that there is no actual good reason demonstrated for that epsilon and that the documentation specifies the return of a zero length vector when the vector can't be normalised when the actual behaviour is for zero length vectors to be returned even if they can be normalised. And yet there is still resistance to the idea that this is fundamentally wrong. And that's my beef.
Your code example is not the same as $$anonymous$$e. The expression assigning to f is done in a context of 'float' and so the entire calculation is performed as a float.
If you place the expression in the Sqrt function, however, it will promote all elements to double before commencing the calculation, because the context is now 'double'.
Try it and see.
Your answer