koobas.hobune.stream
What is affected by the W in Quaternion(x,y,z,w)?
I'm just wondering what is affected by the 'w' parameter in Quaternion...
a quaternion is a complex number with w as the real part and x, y, z as imaginary parts.
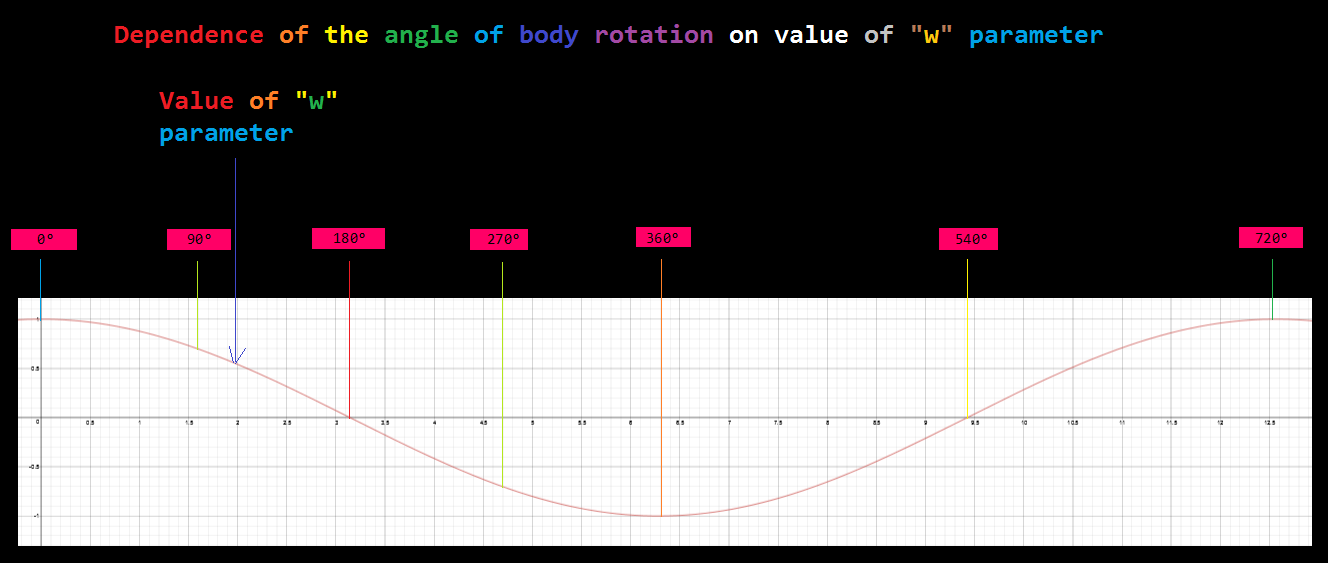
If a quaternion represents a rotation then w = cos(theta / 2), where theta is the rotation angle around the axis of the quaternion.
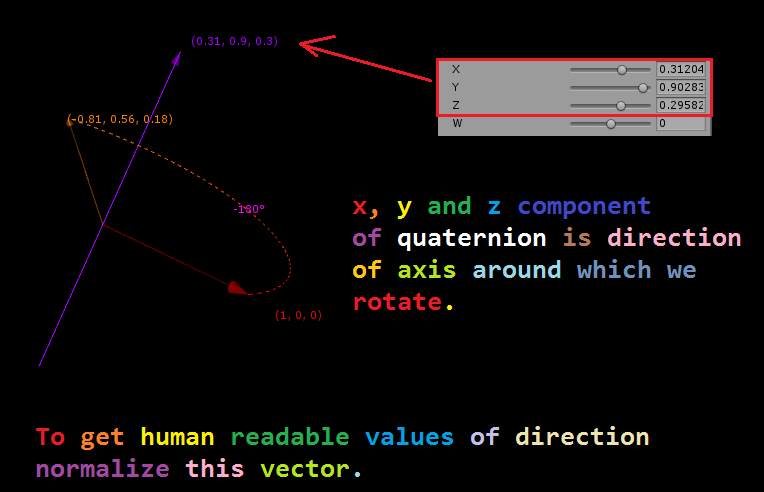
The axis v(v1, v2, v3) of a rotation is encoded in a quaternion: **x = v1 sin (theta / 2), y = v2 sin (theta / 2), z = v3 sin (theta / 2)*.
If w is 1 then the quaternion defines 0 rotation angle around an undefined axis v = (0,0,0).
If w is 0 the quaternion defines a half circle rotation since theta then could be +/- pi.
If w is -1 the quaternion defines +/-2pi rotation angle around an undefined axis v = (0,0,0).
A quater circle rotation around a single axis causes w to be +/- 0.5 and x/y/z to be +/- 0.5.
Kind Regards, Keld Ølykke
Quaternions are four-dimensional, so you need four properties. The x/y/z properties don't correspond to x/y/z in euler angles. With quaternions, each of the properties is a normalized float between 0 and 1, so for example a euler angle of 45/90/180 is represented by a quaternion as approximately .65/-.27/.65/.27.
If you don't already know, it's not something that's easily explained unfortunately.
$$anonymous$$ade my day ;) As one of the most useless comments out there. Why bother?
You may better watch the numberphile video on quaternions. Dr James Grime does a great job explaining the very basics.
