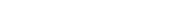What do the values in the Matrix4x4 for Camera.projectionMatrix do?

I try my best to explain the projection matrix and it's values.

First of all you should understand that a matrix is one mathematical object / construct which can be used to perform a linear transformations. The most important operation you can do with matrices is the matrix multiplication. Some distinguish between matrix-matrix multiplication and matrix-vector multiplication but a vector actually is just a special kind of matrix (with just one row or column). Even the vector dot product is just the matrix multiplication between a row vector and a column vector.

Matrix basics

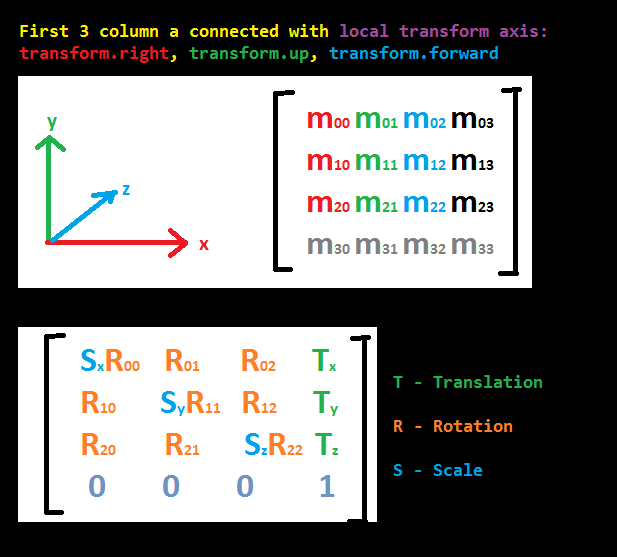
Matrix layout in Unity

Unity uses a Column major layout. That means the first 4 variables in memory form the first column. See the following table and note the indices. This might be relevant if you need to pass a Matrix4x4 to native code.

Structure:

 //  member variables |      indices
 // ------------------|-----------------
 // m00 m01 m02 m03   |   00  04  08  12
 // m10 m11 m12 m13   |   01  05  09  13
 // m20 m21 m22 m23   |   02  06  10  14
 // m30 m31 m32 m33   |   03  07  11  15
 
 M[RowIndex, ColumnIndex] == M[RowIndex + ColumnIndex * 4]

This is the layout of Unity's Matrix4x4 struct. You have to understand that each row and each column corresponds to a certain dimension (x, y, z, w). So the first row and the first column belongs to the "x" component. The second row / column to "y" and so on.

When you multiply a matrix with a vector there are generally two ways to do this. Either "M V" or "V M". Note that those are not commutative. Unity's Matrix4x4 struct only supports "M * V" so the input vector is treated as column vector and the result will be a row vector.

This is how a multiplication of a matrix (M) with a vector (V) looks like:

Matrix multiplication

 P = M * V
 
 (m00, m01, m02, m03)   (V.x)   (m00*V.x + m01*V.y + m02*V.z + m03*V.w)
 (m10, m11, m12, m13) * (V.y) = (m10*V.x + m11*V.y + m12*V.z + m13*V.w)
 (m20, m21, m22, m23)   (V.z)   (m20*V.x + m21*V.y + m22*V.z + m23*V.w)
 (m30, m31, m32, m33)   (V.w)   (m30*V.x + m31*V.y + m32*V.z + m33*V.w)

As you can see our vector is multiplied component wise with the first row of our matrix and the result is added up to a single value. If you imagine the first row of the matrix as a Vector4 it's the dot product between our vector and that first row. This value is the new "X" value of our resulting vector. It's the "X" value because it was the first row of the matrix.

P = M * V could be visualized like this:

 (V.x,  V.y,  V.z,  V.w)
   |     |     |     |
   *     *     *     *
  \|/   \|/   \|/   \|/
 (m00 + m01 + m02 + m03) --> (P.x)
 (m10 + m11 + m12 + m13) --> (P.y)
 (m20 + m21 + m22 + m23) --> (P.z)
 (m30 + m31 + m32 + m33) --> (P.w)

So "V.x" get multiplied with every component of the first column, "V.y" with the second, ... and finally you simply add the 4 columns together.

Matrices are used for various things. The main usage inside a game engine like Unity is as a "Transformation matrix". Such a matrix generally looks like this:

Transformation matrix (TSR matrix)

(TSR = Translation, Scale, Rotation)

 ( RS RS RS | T )
 ( RS RS RS | T )
 ( RS RS RS | T )
   ------------ 
 (  0  0  0 | 1 )

The "RS" part is the combined rotation and scale matrix. The "T" part is the translation part. The rotation and scale matrix is a combination of several rotation matrices (usually one for each plane of rotation which is 3 in 3d space) and a scale matrix.

 // Scale matrix
  SX  0  0
   0 SY  0
   0  0 SZ
 
 //Rotation matrices
   x-y-rotation(z-axis)   |   y-z-rotation(x-axis)   |   x-z-rotation(y-axis)
  ------------------------|--------------------------|------------------------
  ( cos(z), -sin(z), 0 )  |  ( 1,   0   ,    0    )  |  (  cos(y), 0, sin(y) )
  ( sin(z),  cos(z), 0 )  |  ( 0, cos(x), -sin(x) )  |  (    0   , 1,   0    )
  (   0   ,    0   , 1 )  |  ( 0, sin(x),  cos(x) )  |  ( -sin(y), 0, cos(y) )

The combination of those it quite more complicated. For more information see rotation matrix

Projection matrix

The projection matrix plays a special role. It's responsible for projecting 3d coordinates from view / camera space into "normalized device coordinates". However perspective projection requires an operation that isn't possible with pure matrix operations. Specifically in a perspective projection the x and y coordinates have to be scaled based on the z value of the vertex. However a matrix can only create linear combinations (additions) of the different incoming components. Therefore our graphics hardware uses a special convention. It uses homogeneous coordinates where the 4th vector component acts as "normalization value". After the transformation the hardware performs the "homogeneous divide". That is dividing the whole vector by the 4th component (the "w" value)

A trivial perspective projection matrix would look like this:

 ( 1  0  0  0 )
 ( 0  1  0  0 )
 ( 0  0  1  0 )
 ( 0  0  1  0 )

Here the 3d coordinates are just passed through unchanged. However in addition we do not propergate the incoming "w" value (fourth column is 0) but instead we return the incoming "z" value as "w". This has the effect that the resulting vector will be divided by the distance from the camera. So the further away a vertex is, the "smaller" the resulting vector gets. Keep in mind that the origin of our coordinate system is the center of the screen. If you imagine a vector like (12, 20, 3, 1) it would end up at (4, 6.666, 1, 1). If we move the point further away from the camera (from 3 to 4) the result would be (3, 5, 1, 1).

That's basically how perspective projection works. Now focus on the off-center example.

 ( x  0  a  0 )       x = 2*near/(right-left)          y = 2*near/(top-bottom)
 ( 0  y  b  0 )       a = (right+left)/(right-left)    b = (top+bottom)/(top-bottom)
 ( 0  0  c  d )       c = -(far+near)/(far-near)       d = -(2*far*near)/(far-near)
 ( 0  0  e  0 )       e = -1

First ignore "a" and "b" and imagine they are just "0". Now it should be clear that "x" and "y" are just scale factors which will scale the incoming x / y coordinate. "c" and "d" are there to calculate the actual depth value that is written into the depth buffer. "c" is again just a scaling factor of the incoming "z" value and d is a constant offset. Since the incoming "w" value is always "1" it means "d" is just added to the outgoing z value. Finally there's "e" which is just the value "-1" and has the same purpose as i explained in the trivial example. It returns "-z" as "w" in order to perform the perspective divide.

In any usual projection matrix "a" and "b" will be "0" since you usually have the view centered in the screen. However if you want an off-center perspective, those values provide a linear offset. So the incoming "X" value is first scaled by the "x" in the matrix and in addition "a * z" is added as well. So the further away an object / vertex is, the more it is shifted to the right (if "a" is positive) or to the left (if "a" is negative). However since the final position is divided by the z position, that means "X" is simply offsetted by a constant amount in screen coordinates. For example if "a" is "2" and the incoming z value is "12" you will add "24" to the "X" value. After the divide it will be "2" again.

In most cases you don't specify left, right, top and bottom manually. The more common way to specify them is by using a FOV angle and using the aspect ratio of the screen.

left, right, top and bottom actually specify the boundary / size of the near-clipping plane. The "near" distance defines how far away from the camera origin the clipping plane is located.

For example is you use PerspectiveOffCenter like this:

 PerspectiveOffCenter(-1f,1f,-1f,1f, 1f,1000f);

You would create a 90° perspective view in both axis. Note that we don't took the aspect ration into account. So if the screen is not square the image will be stretched. In this case the near clipping plane is a plane of size 2x2 one unit away from the camera origin. That gives you a 45° angle on each side and an overall FOV of 90°.

Since "a" and "b" are defined as:

 a = (right + left) / (right - left);
 b = (top + bottom) / (top - bottom);

it should be obvious that when right and left have equal size (but different signs) they sum up to "0". That's the usual case when the perspective center is in the middle.

The factors "x" and "y" are simply the ratio between the near clipping distance and the view width / height. "(right - left)" would be "2" in our example case since "right" is 1 and "left" is -1.

For more information on projection matrices, see this paper.

ps: If you're wondering why certain values are negative, that's because of convention, again. The normalized device coordinates uses a left-handed system while OpenGL (and mathematics in general) uses a right-handed system. Unity however already uses a left-handed system. But since the projection matrix should be compatible with all sorts of APIs, they define it the usual way. That's why Unity's "camera / view matrix" artifically inverts the z-axis. That means inside the shader after the model and view transformation the z values are actually negative.

If you have trouble calculating your projection matrix based on an angle, have a look over here