- Home /
Circular motion via the mathematical circle equation?
I'm looking for a way to create a circular motion for an object. I got the linear and wave (sin) motions working fine. I pretty much know their equations, and they're actual functions (for each point of the graph in x, there's one and only one corresponding point in y - which is the definition of a function) - But the circle isn't a function, since foreach point in the graph, there are two corresponding y values.
From my dusty math knowledge, the equation of the circle is:
x^2 + y^2 = r;
How to get this formula to work in code?
What I have is, an abstract Movement class, that other types of movements inherit from, and override the method GetY - so LinearMovement's GetY just returns the the y value of the velocity, etc. Here's the virtual moving method in the abstract Movement
protected virtual void Move()
{
velocity.y = GetY();
cachedTransform.localPosition += (velocity + direction) * Time.deltaTime * speed;
// more unrelated stuff
}
GetY for the sine movement:
protected override float GetY()
{
return Mathf.Sin(2 * Mathf.PI * Time.time * frequency) * wavelength;
}
GetY for the linear movement:
protected override float GetY()
{
return velocity.y;
}
Now, what I tried to do for my circular movement, is return:
sqrt(r - x * x);
But it didn't give me the right movement.
Please don't give answers related to any of the rotation methods (transform.Rotate, transform.RotateAround, etc) - cause that's not the point of this question.
Thanks for any tips.
EDIT:
if you're curious where I get direction from:
protected virtual void InitDirection()
{
// just get some random orientation for the point/object to face to start moving
float randZ = Random.Range(minInitialOrientation, maxInitialOrientation);
direction = Quaternion.Euler(0, 0, randZ) * cachedTransform.right;
}
I don't exactly understand what you're trying to do. but the circle equation you have is wrong. for a circle with a center (a,b) and radius R the equation is:
R^2 = (x-a)^2+(y-b)^2
so fo the center (0,0) and radius R you get: R^2 = x^2+y^2
and y=sqrt(R^2-x^2)
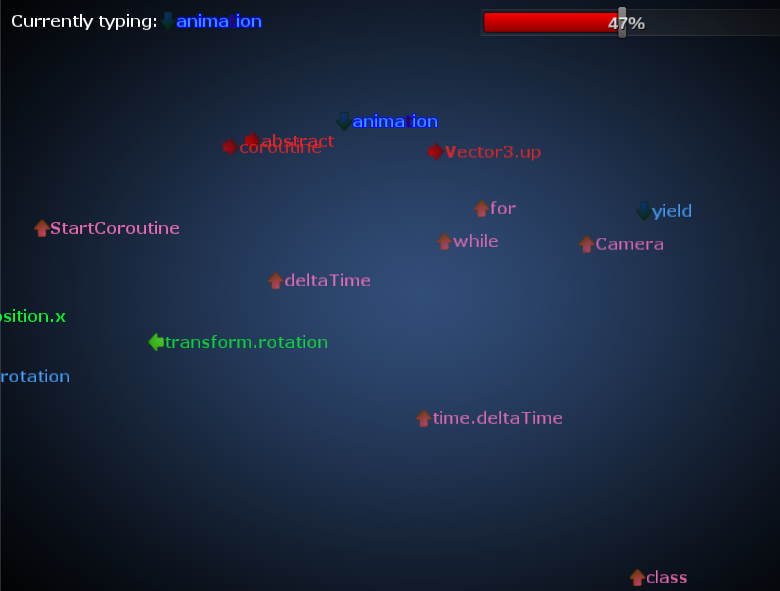
Thanks for your reply. To answer your question, we're working on a simple 2 days game jam - the idea is to have floating text that moves in many ways on the screen. You have to type text, to move your player around. Each text color will move the player to a direction (indicated by the arrow besides the text) - What's related here, is that the text moves in many motions, linearly, sinly, etc.
And yes... you are correct about the equation. I'll try it out now.
Thanks for anybody who answered. I'll be with you in some time to give feedback.
Answer by ziv03 · Dec 14, 2013 at 02:44 PM
I understand now, what you need to use an angle and a radius to calculate the position. you need to increase/decrease the angle every frame, and then calculate the position using these formulas:
x=cos(angle)*R;
y=sin(angle)*R;
for example:
float angle =0;
float speed=(2*Mathf.PI)/5 //2*PI in degress is 360, so you get 5 seconds to complete a circle
float radius=5;
void Update()
{
angle += speed*Time.deltaTime; //if you want to switch direction, use -= instead of +=
x = Mathf.Cos(angle)*radius;
y = Mathf.Sin(angle)*radius;
}
I didn't tested it, but change it to fit your values and it should work. oh and btw, this is for the center (0,0). if you want the circle center to (a,b) you need to change the formulas to:
x=cos(angle)*R+a;
y=sin(angle)*R+b;
FRE$$anonymous$$IN' AWESO$$anonymous$$E! That was the coolest circlish thing I've ever seen XD - Using sin and cos to simulate a circle movement taking advantage that the sin/cos values, form a circle! (the trigonometric circle)
Hi, I was looking for something similar but I am simulating a planet which will be added by players. So when they add more planets around the sun they start moving in equidistance from each other. For example 2 planets will be at an angle of 180 degree from each other and 4 planets will at 90 degrees from each other w.r.t sun. And continue to move. How do i make that? Any suggestion or math topic i should be learning about? Thanks
Thanks very much @ziv03 thats work like a charm! Can you tell that how to do this just by adding force?, and i want to keep ball moving its own direction and at same time rotates too(something like drift).
Answer by KellyThomas · Dec 14, 2013 at 02:49 PM
Note: I'm not entirely sure I understand the question so if this is off topic please take it with a grain of salt.
Your sin function is generating a Y value as a function of time i.e.:
y = Mathf.Sin(2 * Mathf.PI * Time.time * frequency) * wavelength
This is also the y position for a point moving in a circle of a radius equal to wavelength at the given frequency.
The equivalent cos function will return the x position given the same parameters i.e.:
x = Mathf.Cos(2 * Mathf.PI * Time.time * frequency) * wavelength
You were mentioning that a circle is not a capital-F Function due to having two y values for a given x. While this is true, the y values for a given x can be found by the following:
y = (+/-) sqrt(r*r - x*x)
Or the x values for a given y:
x = (+/-) sqrt(r*r - y*y)
@vexe - a parametric equation of a circle will work which is what @$$anonymous$$elly$$anonymous$$ has outline for you here:
http://www.mathopenref.com/coordparamcircle.html
You don't need the '2 * $$anonymous$$athf.PI' unless you are trying to match radians to some other calculation.
@robertbu:
Well $$anonymous$$athf.PI*2 is just another constant factor and considering the name of his variable "frequency" you need it if you're aimng for a certain angular velocity.
@Bunney83 - Understood. But for what he is doing here, I don't believe he needs it. I didn't say it very well, but the only reason I could see to include the constant is if he had other angular calculation that he was trying to match to this calculation. I think all he needs is:
y = r * $$anonymous$$athf.Sin(Time.time * speed);
x = r * $$anonymous$$athf.Cos(Time.time * speed);
For my part I just did a copy paste from question above, as it meant to join a set of movement profiles I thought it best not to introduce or redefine anything unnecessarily.
However I would consider it perfectly reasonable if structured like this:
float radiansPerRotation = 2 * $$anonymous$$athf.PI;
float currentRotations = Time.time * frequency;
float angle = radiansPerRotation * currentRotations;
float y = $$anonymous$$athf.Sin(angle) * radius; //swap in radius for wavelength
It only looks a bit odd when it's all packed into one line.
If I was going to question a component of the original formula, it would be that the term wavelength appears to be used incorrectly. Its function in the formula is to define the peak amplitude, a value that has no baring on the true wavelength.
Correct me if I'm wrong, but I think LD is when you make a game on your own. Game jam is when you make it with a partner.
Whatever it's called, it went pretty well actually. The beauty of the experience was that our tasks were completely separate - I worked on my part, and my partner worked on his. No collisions. Also, we had a 2-days constraint - when you have such a tight schedule, you become really focused into finishing your part - and you will be surprised that you will, in very short time.
Another beauty is that, when you're making something like this, you don't focus on creating highly polished code from the start (that doesn't mean that you should try to your best to apply good code quality habits) - ins$$anonymous$$d, you just write a "working" code, which means you're more making a prototype, than a full game.
It's a nice experience, I highly recommend everybody to engage in it if they have some sort of programmer partner.
Also, we might make a few more, and then make tutorials about our parts - so each programmer makes a video explaining what and why he did what he did. In a way it'd educational, and helps the tutor. Another possible good thing, is that after you and your partner finishes, you could take some time to refactor and polish your codes, after which both of you take a look at eachother's code and criticize where it's due. This leads to a wonderful learning experience where everybody benefits from.
Answer by Tomer-Barkan · Dec 14, 2013 at 02:13 PM
The easiest way to implement circular motion in unity would be to create an empty object in the circle center, then make your object a child of that empty object, then rotate the parent empty object every frame, which will cause your object to rotate around it since it's a child object.
If you want to calculate the motion manually, you can use the physics of circular motion. You can read the formulas here.
Now, to implement it, you could give your object a rigidbody, and then set the velocity to be 90 degrees from the radius (the vector connecting your location and the center. Then, each frame, as the physics engine moves your object according to the velocity, you apply an acceleration towards the center of the circle equal to v^2 / R, where v is the magnitude of rigidbody.velocity, and R is the magnitude of the radius vector.
void ApplyCircularAcceleration(Vector3 center) {
vector3 toCenter = center - transform.position;
rigidbody.velocity += toCenter.normalized * rigidbody.velocity.sqrMagnitude / toCenter.magnitude;
}
if you don't want to use rigidbody, you could keep your own velocity vector, and move the object each frame according to that velocity.
Sorry for late reply. Thanks for your answer +1. I will definitely check that approach out.
Hi, I was looking for something similar but I am simulating a planet which will be added by players. So when they add more planets around the sun they start moving in equidistance from each other. For example 2 planets will be at an angle of 180 degree from each other and 4 planets will at 90 degrees from each other w.r.t sun. And continue to move. How do i make that? Any suggestion or math topic i should be learning about? Thanks
Answer by ForbiddenSoul · Dec 29, 2016 at 07:34 AM
Glad you found an answer already.
Another thing worth looking into is a "spherical interpolation", or "slerp" . Unity includes it for use with circular motion and curves.
https://docs.unity3d.com/ScriptReference/30_search.html?q=slerp
Your answer