- Home /
Transform angle to grid position
Hi, how do I get/transfrom an angle to a "grid direction"...
Getting the angle between two vector3 is simple:
// Get the angle to the target
Vector3 targetDir = target.position - transform.position;
Vector3 forward = transform.forward;
float angle = Vector3.Angle(targetDir, forward);
The problem is that I need to determin from which direction based on nine squares around the target a shoot is comping from.
Look at this image:
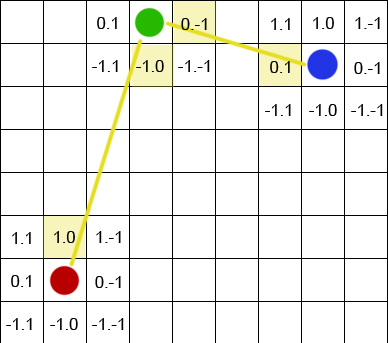
If red is shoot at from green I want to know that the shoot was coming from 1,0.
If Green is shoot at from blue I want to know that the shoot was coming from 0,-1.
Etc...
Is there a way to do this in a simple way?
I got code for transforming positions into "grid position" and to finding the "nine adjecent" grid position and determing which one if 1,1 0,-1 etc. But can't get this to work.
I hope someone understands what I need, in the end it will be for the cover system of an turn-based rts game. This is sort of the last pice of the puzzel.
Answer by whydoidoit · Dec 27, 2012 at 08:01 AM
So you should just be able to take 22.5 from the angle (which is 360/(8*2)), if the result is less than 0 then add 360, then divide the answer by 45 and take the integer as a lookup into an array of coordinates. However Angle returns the angle between a line and another line - which can never be more than 180 degrees. So you also need to know on which side of the red dot, the green dot lies so you can add to the angle.
CS
//Define the angle pairs as shown in your diagram, starting from upwards
Vector2[] angles = new [] { new Vector2(1,0), new Vector2(1,-1), new Vector2(0,-1) ... }
//Get the angle
var angle = targetDir.x < 0 ? 180f + (180f - Vector3.Angle(targetDir, forward)) : Vector3.Angle(targetDir, forward);
//Convert it into an index
var angleIndex = Mathf.FloorToInt((angle < 22.5f ? 360f + angle - 22.5f : angle - 22.5f)/45);
//Get the directions
var direction = angles[angleIndex];
I made a longer answer but it seems to have disappeared: I uploaded the code and it can be played here: http://www.veus.se/Games/TurnBasedRTS1/TurnBasedRTS.html
"Left click" a soldier and move it around by "right clicking" the ground. The red Squares with a hole in it represents the Squares your code return. In the upper left the angle is printed.
Yeah it needs to be using "real" forward not transform.forward (as in the direction vector that in the world implies up the screen). I wasn't aware you were rotating your characters/forgot that you were using transform.forward.
I'm afraid I don't follow when you say the "real" forward. I'm actually more interested in the square that the soldier is standing on as the Soldier should be able to be anything and be rotated in whatever direction.
Yes I know that - which is why using transform.forward doesn't work - you need to measure the angle from straight up the screen. What direction is that? It might be Vector3.forward if up the screen is in + z or it might be Vector3.up if up the screen is measured in + y.
In your diagram - what world coordinate change is incurred to move the red dot one space directly upwards (to your 1,0 square).
Answer by Golan2781 · Dec 29, 2012 at 07:55 PM
You can determine the relative angular direction of two vectors in the XY-plane using the cross product's Z component (respectively for permuted coordinates). This is apparent if you think of the cross product relation in calculating a surface normal of two vectors or a rotation. If you know you are only working with a 2D plane, this calculation is enough:
var clockwise = true;
if (vec1.y*vec2.x > vec1.x*vec2.y)
clockwise = false;
If you only need world coordinates (i.e. direction 'up' instead of 'forward') you already know one vector for sure (e.g. 'up' is 0,1) so the calculation gets really simple - check whether the horizontal axis (whichever corresponds to -90° and +90°) is positive or negative
Of course, there are other ways to achieve what you want. Assuming you only need world directions:
The arctan of the relative (x/y) will give you the proper angle with proper sign.
You can alternatively try and catch the respective cases directly from the relative coordinates. For example, if y<0 it must be one of the lower fields; you can do this for all coordinates and directons. It would be adviseable to do some kind of normalizing between the two directions, so that for example -9/9 is the same as 1/1 and you probably want treat intermediate values such as 4/3 or 1/0.75 as 'upper right'.
Personally, I'd go for the manual cross product, it should be the most performant solution.
Your answer

