Unit 15 Section 2 : Multiplying and Dividing using Negative Numbers

In this section we look at how to multiply and divide when both negative and positive numbers are involved.
We already know how to multiply and divide positive numbers, and working with negative numbers is quite similar.

Example 1
We will start by trying to work out the answer to 5 × (-4).
First of all, think about the sum 5 × 4. The answer is 20.
This is the same as 4 + 4 + 4 + 4 + 4, which gives 20.
In the same way, the sum 5 × (-4) can be written (-4) + (-4) + (-4) + (-4) + (-4), which gives -20.

We can see from this that:
5 × 4 (a positive number multiplied by a positive number) gives 20 (a positive answer).
5 × (-4) (a positive number multiplied by a negative number) gives -20 (a negative answer).

Example 2
Now we will work out the answer to (-4) × 5.
Multiplications work both ways round, for example 3 × 4 is the same as 4 × 3.
In the same way, (-4) × 5 must be the same as 5 × (-4).
We already know that the answer to this is -20.

Now we can see that:
(-4) × 5 (a negative number multiplied by a positive number) gives -20 (a negative answer).

 

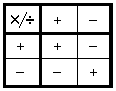Rules for Multiplication and Division
We can summarise the rules for multiplying and dividing two numbers as follows:
If the signs are the same (both positive or both negative), the answer will be positive.
If the signs are different (one positive and one negative), the answer will be negative.

Example 3
Work out the answer to (-4) × (-5).
We start by doing the multiplication without the signs: 4 × 5 = 20.
The table above tells us that a negative number multiplied by a negative number gives a positive answer.
We can now see that the answer to (-4) × (-5) must be 20.

Example Questions

In each question below, you should start by multiplying or dividing the numbers as normal, ignoring the signs.
You should then work out whether the answer is positive or negative using the rules given above.
After you have worked out each answer, click Click on this button below to see the correct answer to see whether you are correct.

(a) 5 × (-7)
(b) (-3) × 4
(c) (-3) × (-5)
(d) 20 ÷ (-4)
(e) (-14) ÷ 2
(f) (-12) ÷ (-3)

 

Exercises

Work out the answers to the questions below and fill in the boxes. Click on the Click this button to see if you are correct button to find out whether you have answered correctly. If you are right then will appear and you should move on to the next question. If appears then your answer is wrong. Click on to clear your original answer and have another go. If you can't work out the right answer then click on Click on this button to see the correct answer to see the answer.

Question 1
Work out the answers to the following multiplications without using a calculator:

(a) (-7) × 2 =
(b) (-4) × 8 =
(c) (-2) × (-5) =
(d) (-6) × (-3) =
(e) (-3) × 7 =
(f) (-10) × (-4) =
(g) 8 × 4 =
(h) 3 × (-6) =
(i) (-7) × (-2) =
(j) (-4) × (-5) =
(k) (-7) × 0 =
(l) 8 × (-5) =

Question 2
Work out the answers to the following divisions without using a calculator:

(a) (-10) ÷ (-2) =
(b) (-15) ÷ 5 =
(c) 18 ÷ (-3) =
(d) 14 ÷ (-7) =
(e) (-21) ÷ (-3) =
(f) (-45) ÷ 9 =
(g) 50 ÷ (-5) =
(h) (-100) ÷ (-4) =
(i) 80 ÷ (-2) =
(j) 26 ÷ (-13) =
(k) (-70) ÷ (-7) =
(l) (-42) ÷ 7 =

Question 3
Complete these multiplication tables:
(a)
×
1
2
3
4
-1
-2
-3
-4
(b)
×
1
0
-1
-2
-3
-4
-2
0
1

Question 4
Complete these multiplication tables:
(a)
×
-1
2
-2
2
-3
-9
(b)
×
-2
10
-2
6
3
-12

Question 5
Fill in the missing numbers in these calculations:

(a) × 5 = -20
(b) (-80) ÷ = 4
(c) 16 × = -32
(d) (-4) × = 32
(e) × (-3) = 12
(f) 40 ÷ = -8
(g) -8 × = 48
(h) -32 ÷ = 4
(i) 15 × = -60
(j) 100 ÷ = -25

You have now completed Unit 15 Section 2
Your overall score for this section is
Correct Answers
You answered questions correctly out of the questions in this section.
Incorrect Answers
There were questions where you used the Tell Me button.
There were questions with wrong answers.
There were questions you didn't attempt.
Feedback on '+tands+''); fbwin.document.write(''); fbwin.document.write(''); fbwin.document.write('
We appreciate any comments you have '); fbwin.document.write('about '+tands+'. We are particularly interested in mathematical errors or aspects of the '); fbwin.document.write('page which could be confusing.
'); fbwin.document.write(''); fbwin.document.write('If you were happy that the unit worked correctly, please click the button on the right. If you '); fbwin.document.write('found any problems or would like to add any comments, please fill out the form below and click '); fbwin.document.write('on the send button.'); fbwin.document.write('
'); fbwin.document.write(''); fbwin.document.write(''); fbwin.document.write(''); fbwin.document.write(''); fbwin.document.write('
'); fbwin.document.write('

'); fbwin.document.write('
'); fbwin.document.write(''); fbwin.document.write(''); fbwin.document.write(''); fbwin.document.write('
'); fbwin.document.write(''); fbwin.document.write(''); fbwin.document.write('Section:
Your name:'); fbwin.document.write('
'); fbwin.document.write(''); fbwin.document.write('Your e-mail:
Comments:'); fbwin.document.write('
'); fbwin.document.write('
'); fbwin.document.close(); }
Since these pages are under development, we find any feedback extremely valuable. Click here to fill out a very short form which allows you make comments about the page, or simply confirm that everything works correctly.
Return to the Tutorials Menu
Produced by A.J. Reynolds January 2001